Исследование модели Ньюмана биологической эволюции
Отметим, что автор модели исследовал экспоненциальное распре-
деление шоков при
= 1
/
20
, что привело к получению ошибочной
оценки
t
≈
1
,
85
, определенной как угловой коэффициент участка гра-
фика, наиболее близкого к линейному в двойном логарифмическом
масштабе.
Принимая в качестве шока минимальное из равномерно распре-
деленных случайных чисел, не получаем ничего принципиально но-
вого. Как следует из рис. 3, степенных графиков с теоретически
предсказанным показателем
t
= 2 + 1
/
(
−
1)
не наблюдается. При
малых формула (9) вообще оказывается неприменима. Условие
разделения (2)–(3) устанавливает ограничение на параметры модели
1
−
−
1
/
≪
1
, которое при разумных размерах экосистемы требу-
ет использования нескольких десятков случайных чисел, что делает
распределение минимума мало отличимым от экспоненциального
с точки зрения свойств модели.
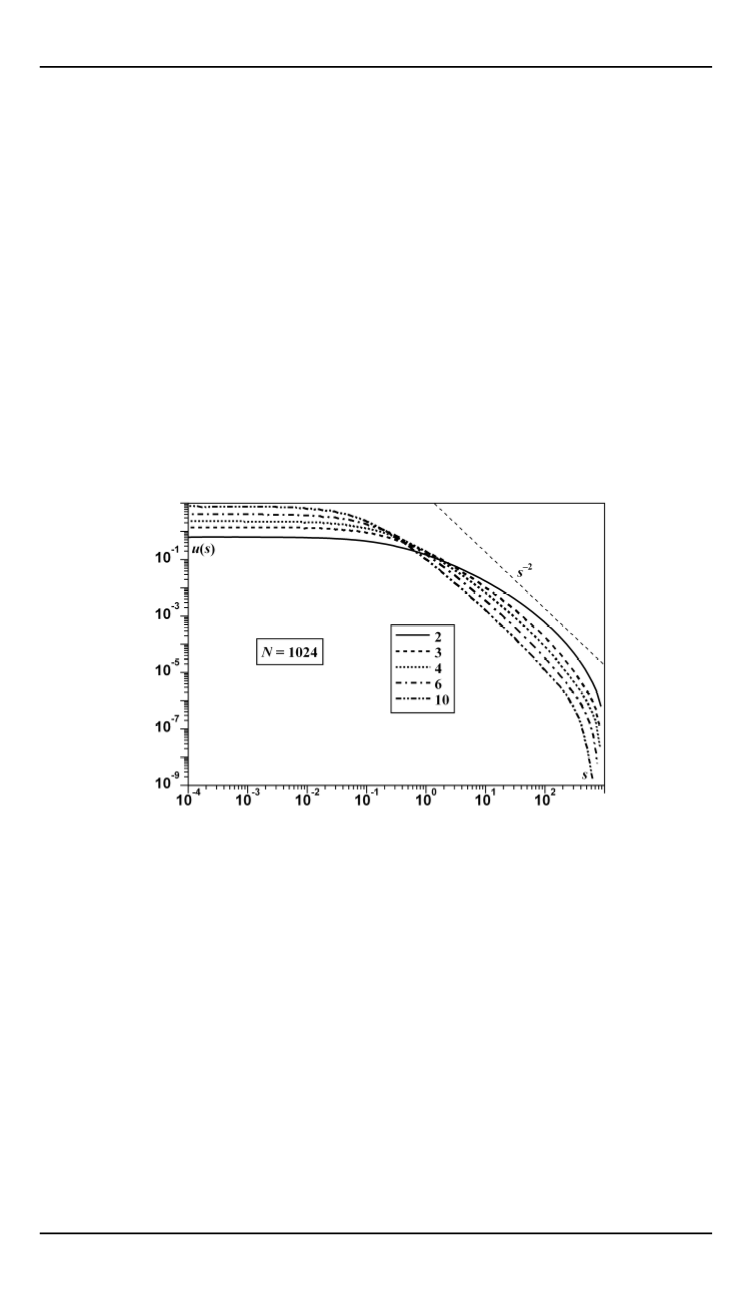
Рис. 3.
Вымирания для распределения шоков, рассчитываемых как минимум из раз-
личного количества числа равномерно распределенных случайных чисел. При ис-
пользовании небольшого количества чисел плотность вымираний весьма далека от
степенного вида. А более-менее степенное поведение начинается лишь при
≈
10
,
когда показатель уже слабо отличим от 2
По всей видимости, не имеет смысла рассматривать и более слож-
ные функции из семейства (10) при
>
0
. Все они позволяют по-
лучить распределения вымираний с показателем
t
>
2
, при котором
средний размер события практически не зависит от размера экосисте-
мы, что нефизично.
Степенное распределение шоков.
Совершенно иной оказывает-
ся ситуация в случае распределения Парето. Как можно увидеть на
рис. 4, при любых значениях
a
плотность распределения вымираний
хорошо приближается степенной зависимостью (9) с предсказанным
9


