Исследование модели Ньюмана биологической эволюции
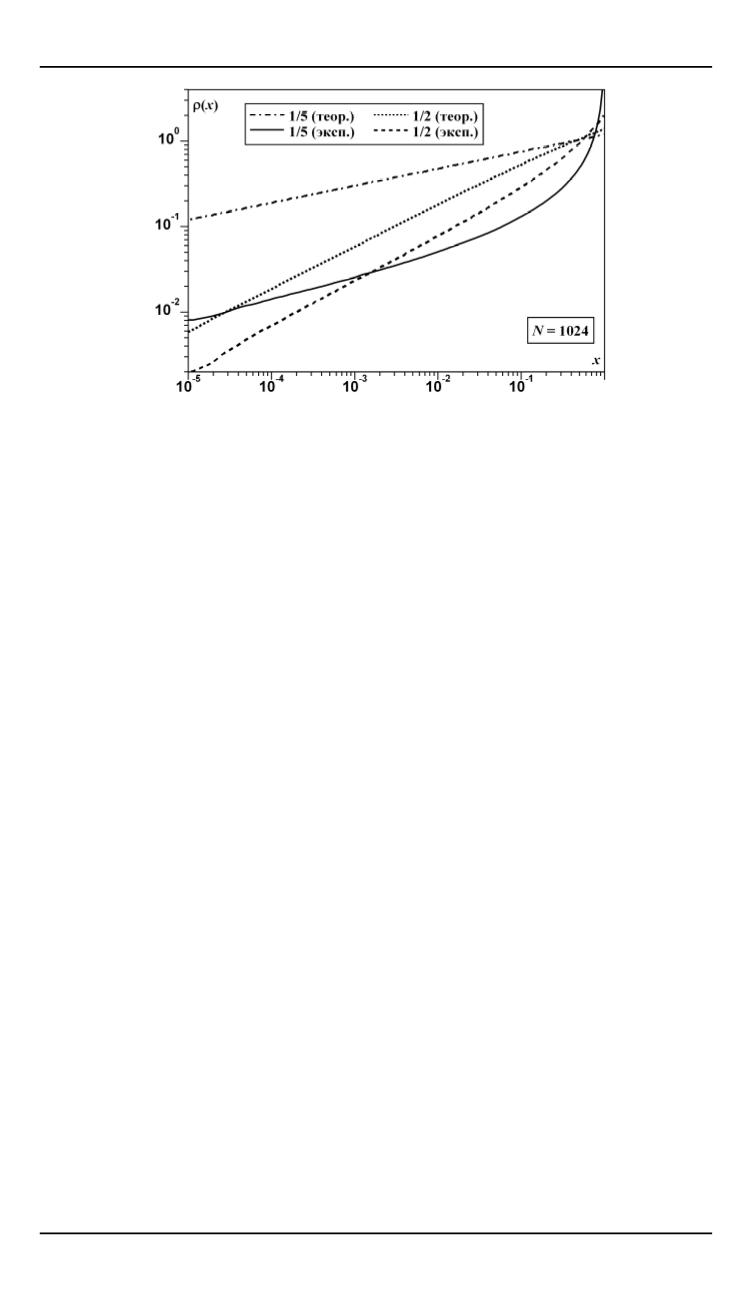
Рис. 7.
Стационарное распределение видов по устойчивости для шоков, распреде-
ленных по Парето с малыми показателями. Теоретические и экспериментальные
графики параллельны в двойном логарифмическом масштабе на большей части диа-
пазона изменения аргумента
экспоненциального распределения шоков этот результат является точ-
ным, а для других распределений плотность вымираний имеет мед-
ленную мультипликативную поправку.
В случае распределения Парето с показателем
a
вымирания распре-
делены степенным образом с показателем
t
= 2
−
1
/
(1 +
a
)
. Причем
эта формула справедлива как при
a
>
1
, когда выполняется условие
разделения, так и при
a
<
1
, когда оно уже не применимо.
Работа выполнена при финансовой поддержке Российского
фонда фундаментальных исследований (проекты 11-01-00887-а и
13-01-00617-а)
.
ЛИТЕРАТУРА
[1] Bak P., Sneppen K. Punctuated equilibrium and criticality in a simple model of
evolution.
Phys. Rev. Lett.
, 1993, vol. 71, no. 24, pp. 4083–4086.
[2] Бак П.
Как работает природа: Теория самоорганизованной критичности
.
Москва, Либроком, 2013, 276 с.
[3] Newman M.E.J., Roberts B.W. Mass-extinction: Evolution and the effects of
external influences on unfit species.
Proc. R. Soc. B
, 1995, vol. 260, no. 1357,
pp. 31–37.
[4] Newman M.E.J., Sneppen K. Avalanches, scaling and coherent noise.
Phys. Rev. E
,
1996, vol. 54, no. 6, pp. 6226–6231.
[5] Roberts B.W., Newman M.E.J. A model for evolution and extinction.
J. Theor. Biol.
,
1996, vol. 180, no. 1, pp. 39–54.
[6] Newman M.E.J. Self-organized criticality, evolution and the fossil extinction record,
Proc. R. Soc. B
, 1996, vol. 263, no. 1376, pp. 1605–1610.
[7] Sneppen K., Newman M.E.J. Coherent noise, scale invariance and intermittency in
large systems.
Physica D
, 1997, vol. 110, no. 3–4, pp. 209–222.
13


