Исследование модели Ньюмана биологической эволюции
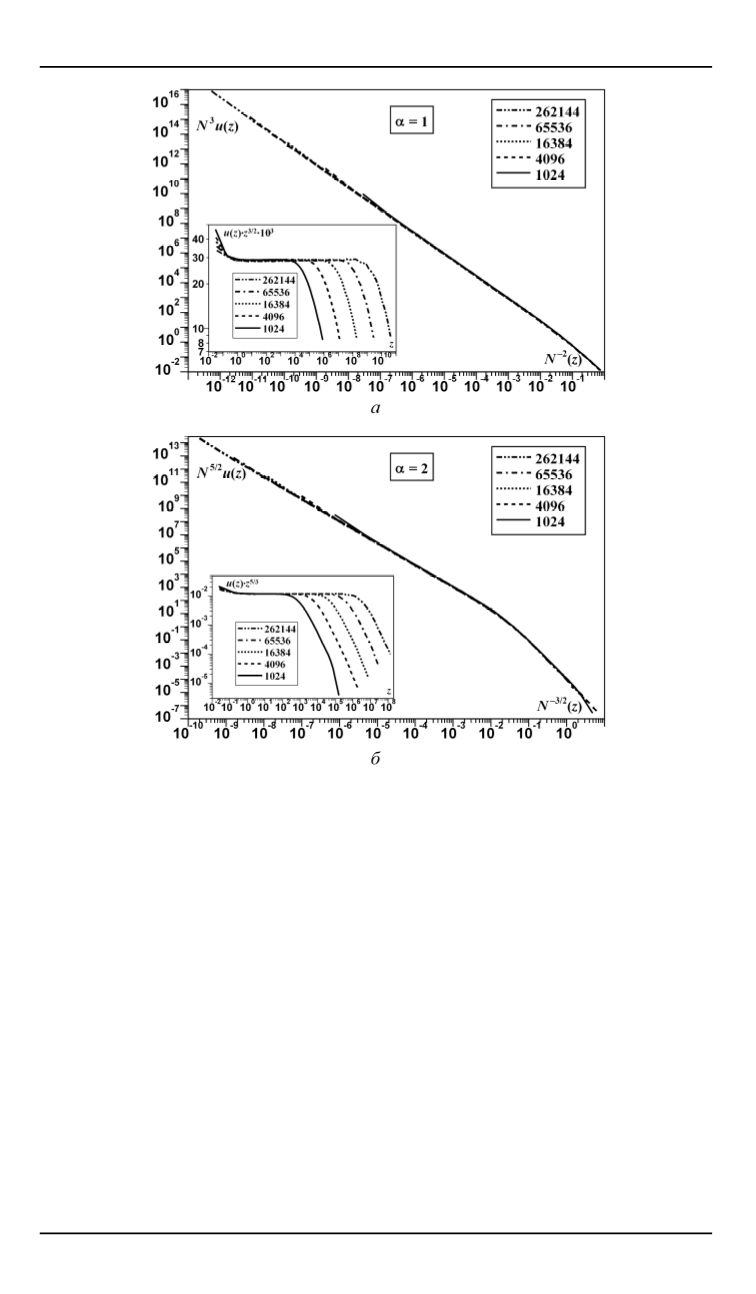
Рис. 5.
Вымирания для распределения Парето шоков при различных размерах
системы: для
a
= 1
совмещение графиков достигается при
n
= 2
,
b
= 3
, что дает
t
= 3
/
2
(
а
); для
a
= 2
совмещение графиков достигается при
n
= 3
/
2
,
b
= 5
/
2
, что
дает
t
= 5
/
3
(
б
)
значение
=
, для которого без изменений применимы все скей-
линговые формулы (рис. 5).
Формула (2) определяет критическую устойчивость
=
0
1
/
a
∼
1
/
a
−
1
.
С помощью формулы (16) получаем соответствующий крупнейший
возможный размер события
max
∼
n
, где
n
= 1 + 1
/
a
. Соотно-
шение (15) позволяет определить второй скейлинговый показатель
b
= 2 + 1
/
a
. Примеры конечно-размерного скейлинга, приведенные
на рис. 5, дают возможность убедиться в правильности этих результа-
тов. Однако справедливы они только для значений
a
>
1
.
При
a
<
1
условие разделения (2), (3) не выполняется из-за неогра-
11


