Г.Г. Малинецкий, А.В. Подлазов
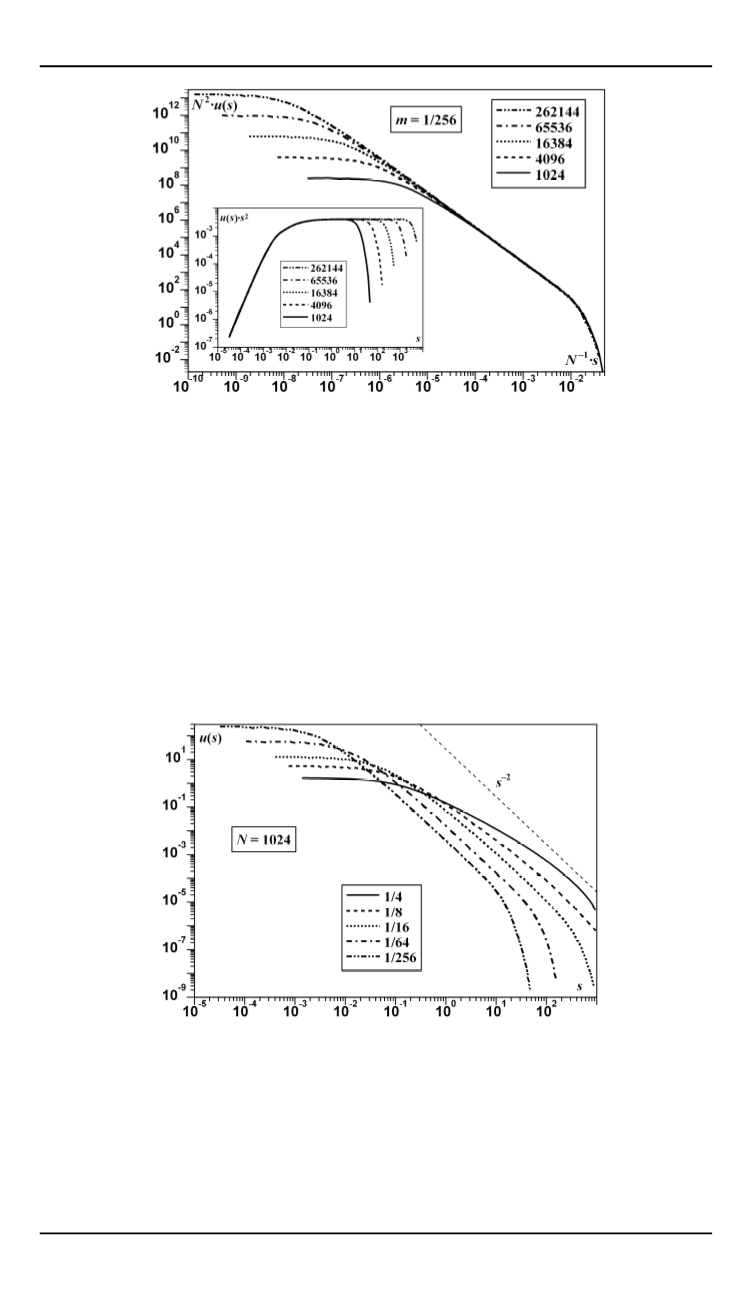
Рис. 1.
Вымирания для экспоненциального распределения шоков при различных
размерах системы. Графики плотностей вымирания совмещаются при конечно-
размерном скейлинге с показателями
n
= 1
и
b
= 2
. Правильность соответствующе-
го им значения показателя распределения
t
= 2
подтверждается врезкой, на которой
плотности домножены на
t
, что приводит к выполаживанию их графиков в про-
межуточной асимптотике. Для данного распределения шоков крупнейшие события
составляют лишь единицы процентов от размера системы, тогда как наименьшие
события, еще описываемые степенным распределением, имеют размер порядка
модельной экосистемы ограничивает средний шок несколькими со-
тыми. При превышении этого ограничения получающаяся плотность
вероятности уже не подчиняется ни формуле (9), ни формуле (14).
Рис. 2.
Вымирания для экспоненциального распределения шоков с различным сред-
ним. По мере увеличения среднего шока графики в промежуточной асимптотике
все сильнее отклоняются от степенного вида, становясь вс¨e более пологими. Это
может быть ошибочно истолковано как уменьшение значения показателя
t
. Как
ориентир нарисована прямая, соответствующая зависимости с показателем
t
= 2
.
При
= 1
/
64
график в промежуточной асимптотике уже практически параллелен
этой линии
8


