Г.Г. Малинецкий, А.В. Подлазов
показателем
t
= 2
−
1
/
(1 +
a
)
. Причем, чем дальше он от двойки,
тем лучше качество приближения, т. е. здесь наблюдается картина,
обратная той, которая наблюдалась для распределения минимума.
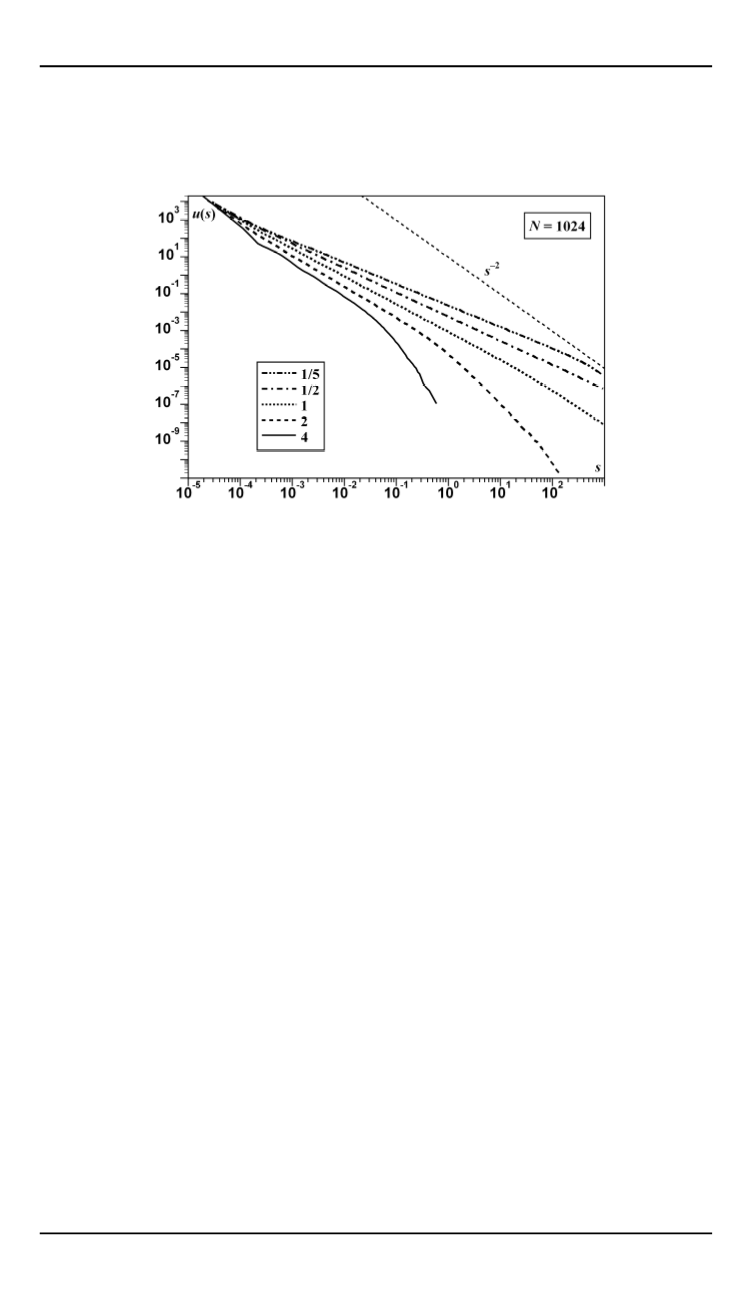
Рис. 4.
Вымирания для распределения Парето шоков с различными показателями.
По мере увеличения показателя распределения шоков
a
показатель распределения
вымираний
t
приближается к 2. Одновременно происходит уменьшение крупней-
шего события
Прежде чем перейти к более подробному анализу результатов, по-
лученных для распределения Парето, рассмотрим использующийся
метод генерации шоков. Поскольку подчиняющиеся этому распре-
делению величины не имеют характерных масштабов, число затро-
нутых карманов гистограммы рассчитывается непосредственно как
−
1
/
a
, где — случайное число, равномерно распределенное на ин-
тервале
(0; 1)
. Таким образом, наименьшее возможное значение шока
0
= 1
/
∼
1
/
, определяющее нормировку распределений, зависит
от размера экосистемы, что необходимо учитывать при проведении
скейлинга. Если пересчитать формулу (8), сохраняя коэффициенты,
получим зависимость вымирания от шока
∼
a
1+
a
.
(16)
При этом распределение (9) принимает вид
( )
∼
( )
−
t
.
Таким образом, графики, полученные при разных значениях , не
совпадают даже в промежуточной асимптотике, вследствие чего соот-
ношение (15) утрачивает применимость.
Наиболее простой способ, позволяющий исправить ситуацию, —
использование в качестве размера события не размер вымирания , а
10


