Г.Г. Малинецкий, А.В. Подлазов
ниченного увеличения с увеличением значения . В результате мо-
дель утрачивает скейлинговые свойства. Тем не менее распределение
событий по-прежнему хорошо аппроксимируется степенной зависи-
мостью с показателем
t
= 2
−
1
/
(1 +
a
)
.
Чтобы понять, почему здесь остаются верными следствия, полу-
чаемые на основе уже неверных посылок, вернемся к распределению
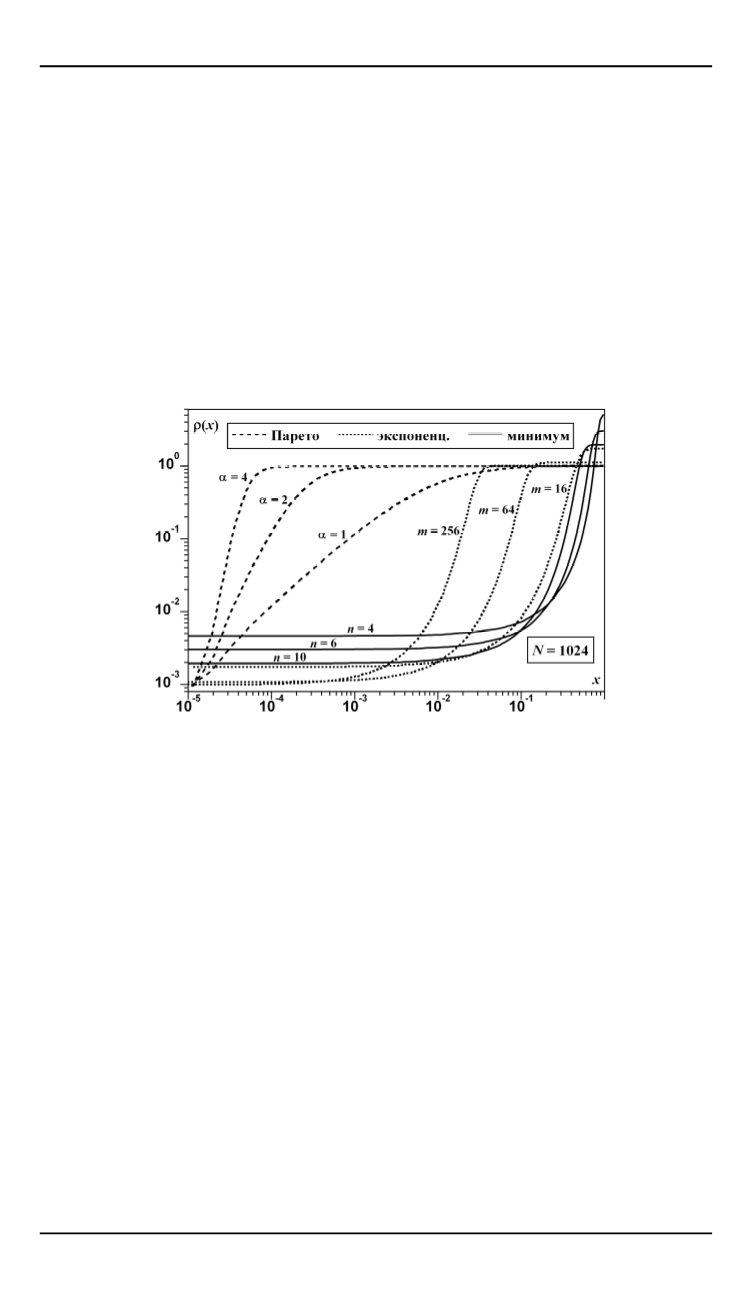
видов по приспособленности (1). На рис. 6 приведены его графики для
некоторых рассмотренных ранее случаев, в которых поведение моде-
ли вполне соответствует нашим ожиданиям. При больших графики
выходят на плато, и вопрос заключается лишь в расположении точки
, где это происходит.
Рис. 6.
Стационарное распределение видов по устойчивости для различных распреде-
лений шоков. Приведенные экспериментальные графики соответствуют формуле (1)
В случае распределения Парето с показателем
a
<
1
не имеет
смысла говорить о стационарном распределении видов по устойчи-
вости из-за регулярного возникновения шоков, уничтожающих всю
экосистему или значительную ее часть. Однако, как показывают ре-
зультаты моделирования (рис. 7), за исключением области самых вы-
соких устойчивостей усредненный график
r
( )
отличается от плотно-
сти, предсказываемой формулой (1), лишь коэффициентом. При этом
вполне естественно, что сохраняется распределение вымираний, оп-
ределяемое с точностью до коэффициента.
Выводы.
Возникновение степенной статистики вымираний в мо-
дели Ньюмана связано с возможностью возмещения вымирающих ви-
дов. Эта возможность обеспечивается выполнением условия разделе-
ния, гарантирующего постоянную скорость видообразования.
Для распределений шоков с быстро убывающей плотностью вы-
мирания распределены степенным образом с показателем
t
∼
= 2
. Для
12


