В.С. Зарубин
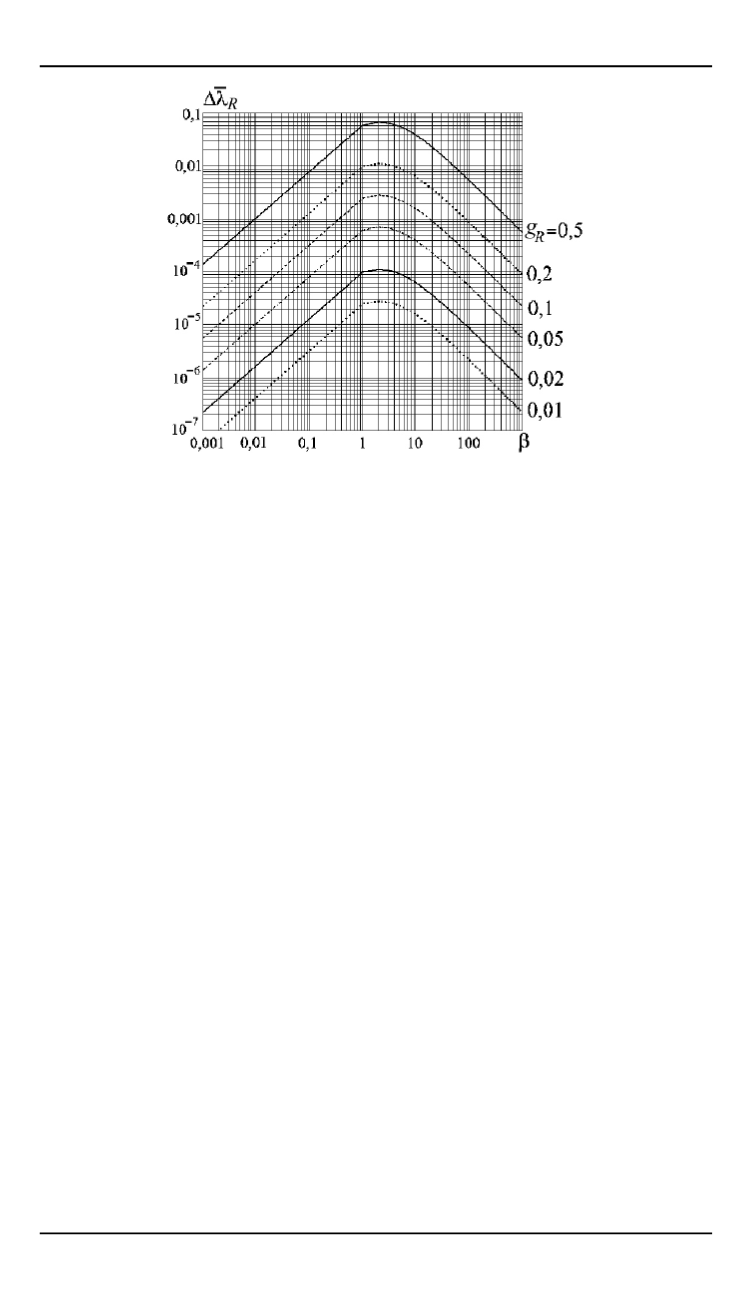
Рис. 4.
Зависимости величины
D
¯
l
от параметра
b
при различных значениях
Таким образом, с достаточно высокой точностью применительно
к реальным ситуациям (
<
0
,
1
) можно положить
¯
l
=
b
, или
l
=
es
0
3
0 0
.
(16)
Формула с такой структурой хорошо известна, но ее вывод в боль-
шинстве работ опирается на математическую модель теплообмена
излучением между двумя параллельными неограниченными пласти-
нами [1–4], зазор между которыми является лишь довольно грубым
приближением к форме замкнутых пор в применяемых в технике ма-
териалах. При этом в качестве характерного размера поры обычно
используют ее размер в направлении наименьшей протяженности.
Для шаровой полости таким размером будет ее диаметр, тогда как
в формулу (16) входит радиус
0
полости. Кроме того, на месте
коэффициента излучения
e
в рекомендованных расчетных форму-
лах [1, 4] стоит приведенный (или эффективный) коэффициент излу-
чения
e
пр
= 1
/
(1
/
e
1
+1
/
e
2
−
1)
, где
e
1
и
e
2
— коэффициенты излучения
поверхностей, между которыми происходит теплообмен излучением.
В случае
e
1
=
e
2
=
e
место
e
в расчетной формуле, аналогичной соот-
ношению (16), занимает коэффициент
e
пр
=
e
/
(2
−
e
)
[2] или равный
ему коэффициент
e
пр
=
e
2
/
(1
−
(1
−
e
)
2
)
[3].
Для полости в виде куба с длиной ребра
ℎ
получена формула [1]
l
= 2
e
1
,
2
s
0
3
ℎ
, где
e
1
,
2
— некоторый приведенный коэффициент из-
лучения в кубической полости, причем верхняя и нижняя грани куба
имеют температуры
1
и
2
соответственно, а а средняя температура
боковых граней
= (
1
+
2
)
/
2
и линейно изменяется по их высоте.
При сравнении этой формулы с соотношением (16) следует отметить,
что величину
2
ℎ
можно рассматривать как эквивалент величины
4
0
.
8


