Оценка эквивалентного коэффициента теплопроводности при. . .
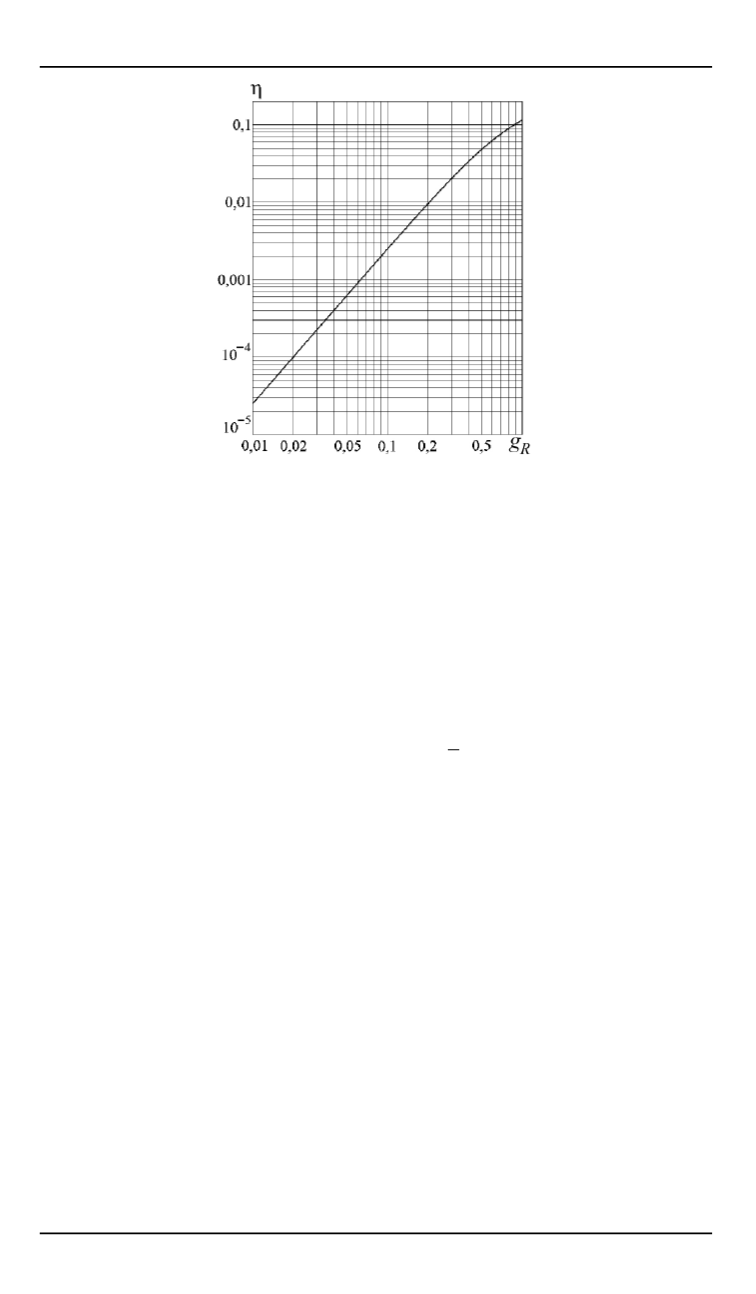
Рис. 3.
Зависимость величины
h
от параметра
рической поверхности при
j
∈
[0;
p
/
2]
, с учетом соотношения (14)
получаем
p
2
0
l
= 2
p
2
0
p
/
2
∫︁
0
¯(
j
) sin
j j
= 2
p
2
0
es
0
3
0
0
(2 +
2
)
,
или, учитывая равенство
= 3
/
(2 + ¯
l
)
,
(2 + ¯
l
)
2
( ¯
l
−
b
) =
9
4
b
2
,
(15)
где
b
= 4
es
0
3
0 0
/
l
.
Из равенства (15) следует, что
¯
l
>
b
при
b
>
0
и
>
0
. Ра-
венство (15) является полным кубическим уравнением относительно
искомого значения
¯
l
. Однако при
<
1
единственный действи-
тельный положительный корень этого уравнения лишь незначитель-
но превышает значение
b
. На рис. 4 в логарифмических координатах
представлены зависимости
D
¯
l
= ¯
l
−
b
от
b
при различных значе-
ниях параметра . Наибольшим значениям
D
¯
l
соответствуют зна-
чения
b
*
≈
2
, а именно:
b
*
≈
2
,
06800
при
= 0
,
5
,
b
*
≈
2
,
01119
при
= 0
,
2
,
b
*
≈
2
,
00281
при
= 0
,
1
,
b
*
≈
2
,
000703
при
= 0
,
05
,
b
*
≈
2
,
0001125
при
= 0
,
02
и
b
*
≈
2
,
00002812
при
= 0
,
01
.
Характерно, что при этом для наибольших значений справедливо ра-
венство
D
¯
l
=
b
*
−
2
. Следовательно, даже наибольшие отклонения
значения
¯
l
от значения
b
быстро уменьшаются с уменьшением па-
раметра . Для гипотетического значения
= 1
имеем
b
*
= 2
,
25
и соответственно
D
¯
l
= 0
,
25
.
7


