Оценка эквивалентного коэффициента теплопроводности при. . .
или, используя формулы (4) и (6), находим
*
ср
=
s
0
(︁
4
0
+ 2
2
0
2 2
0
+
4 4
0
5
)︁
.
(13)
Поскольку
¯ =
e
∘
−
п
, при условиях
=
e
и
*
п
=
*
ср
с учетом
формул (4) и (13) запишем
z
(
j
) =
¯(
j
)
es
0
4
0
= (1 + cos
j
)
4
−
(︁
1 + 2
2
+
4
5
)︁
,
(14)
где
=
0
/
0
6
1
. Из этого равенства следует, что при
cos
j
*
=
(1 + 2
2
+
4
/
5)
1
/
4
−
1
>
0
,
т. е. при
j
*
<
p
/
2
величина
z
(
j
)
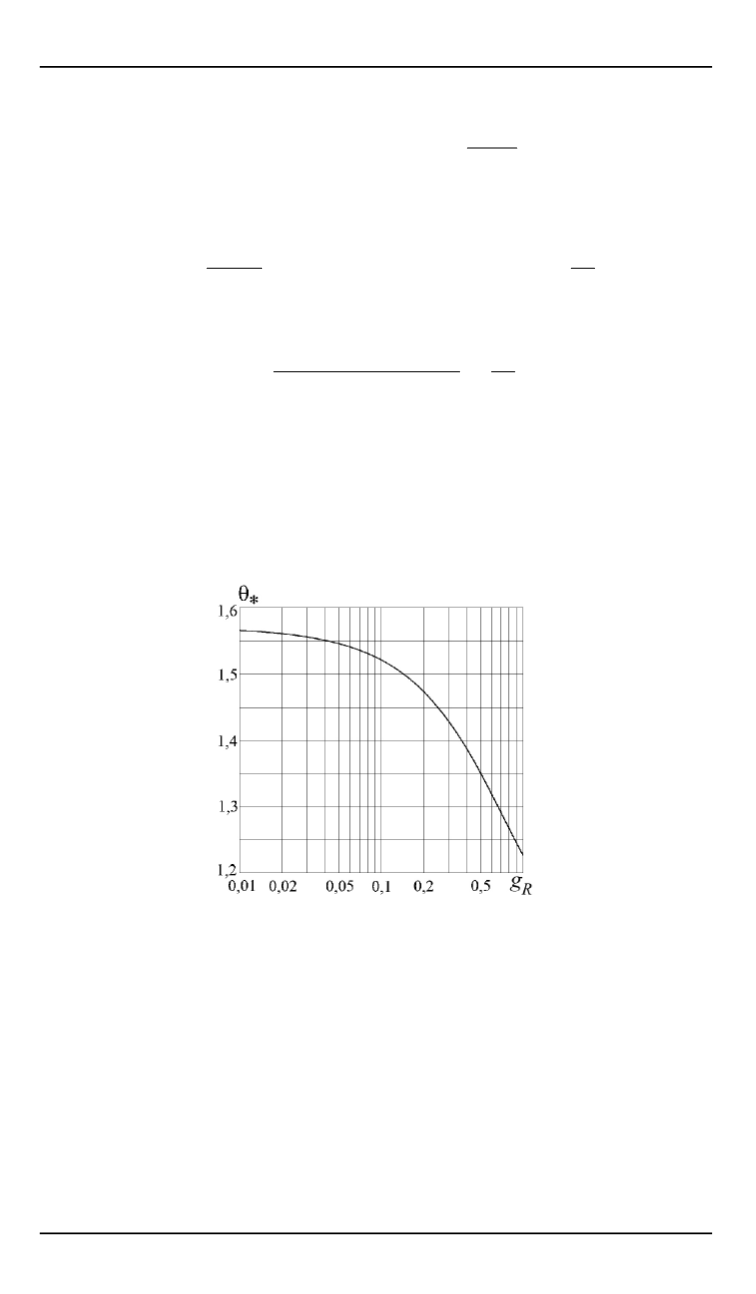
изменяет знак. На рис. 1 в полу-
логарифмических координатах представлена зависимость угла
j
*
от
параметра . При физически допустимом шкалой абсолютных тем-
ператур значении
= 1
имеем
cos
j
*
≈
0
,
33748
и
j
*
≈
1
,
22656
.
Отметим, что при
= 0
,
001
угол
j
*
≈
1
,
5703
, т. е. отличается от
значения
p
/
2
≈
1
,
5708
всего на
0
,
0005
(около
0
,
03
%).
Рис. 1.
Зависимость угла
j
*
от параметра
Таким образом, в общем случае в полуинтервале
(
j
*
;
p
/
2]
измене-
ния угла
j
на сферической поверхности рассматриваемой шаровой по-
лости возникает несоответствие между подводимым к этой поверхно-
сти за счет теплопроводности и отводимым излучением тепловыми
потоками, т. е. происходит локальное нарушение закона сохранения
энергии. На рис. 2 для различных значений параметра приведена
зависимость отношения
¯
z
=
z
(
j
)
/
z
(0)
от угла
j
(в градусах). Там же
тонкой сплошной кривой для сравнения представлен график полувол-
ны косинусоиды, определяющей в безразмерном виде распределение
плотности подводимого к полости при
j
∘
∈
[0; 90
∘
)
и отводимого от
5


