В.С. Зарубин
нее при
j
∘
∈
(90
∘
; 180
∘
]
за счет теплопроводности теплового потока.
Ясно, что при
6
0
,
02
зависимости практически совпадают с ко-
синусоидой, а при
= 0
,
05
некоторое отличие этой зависимости от
косинусоиды заметно лишь при
j
∘
∈
[120
∘
; 180
∘
]
.
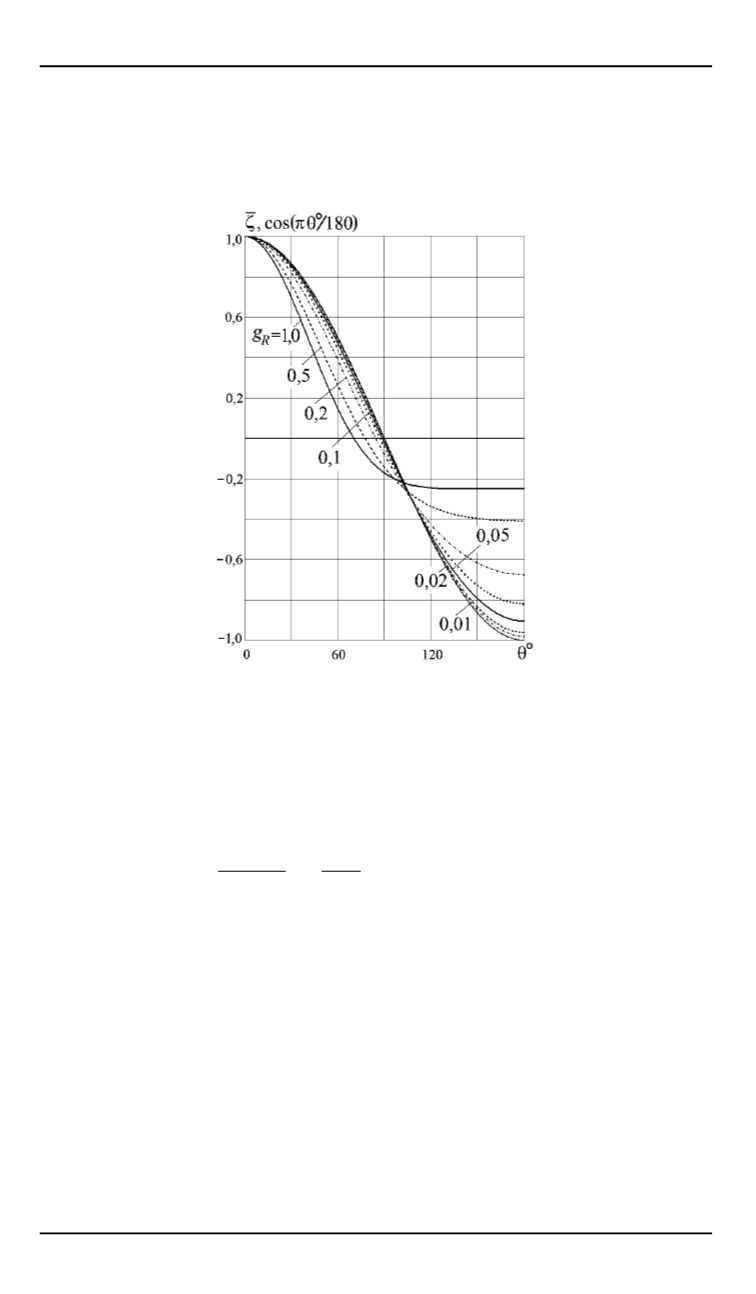
Рис. 2.
Зависимость отношения
¯
z
=
z
(
j
)
/
z
(0)
от угла
j
С учетом формулы (5) доля тепловой энергии, подводимая пу-
тем теплопроводности через участок сферической поверхности при
j
∈
(
j
*
;
p
/
2)
, от всей подводимой к полости энергии составит вели-
чину
h
=
2
p
2
0
l
p
/
2
∫︁
j
*
⃒ ⃒ ⃒ ⃒
=
0
sin
j j
= cos
2
j
*
.
Зависимость величины
h
от параметра представлена на рис. 3
в логарифмических координатах, причем значению
= 1
соответ-
ствует значение
h
≈
0
,
1139
, по которому можно определить предель-
но возможную интегральную погрешность оценки значения
l
при
используемой математической модели.
Эквивалентный коэффициент теплопроводности.
В реальных
ситуациях при сравнительно малых размерах пор в применяемых на
практике материалах
<
0
,
1
и поэтому интегральная погрешность,
оцениваемая значением
h
, будет достаточно малой. Приравнивая теп-
ловой поток , подводимый к полости путем теплопроводности и оп-
ределяемый формулой (5), потоку излучения, теряемому с полусфе-
6


