Применение теории собственных напряжений…
5
τ
τ
1 σ
3
3 ε
ε ,
;
2
i
i
i
i
p
(14)
где
τ τ
σ , ε
i
i
— интенсивности напряжений и деформаций, соответ-
ствующие чистому сдвигу.
Отсюда следует, что кривая
) (ε
i
i
p
с точностью до масштабных ко-
эффициентов 1 / 3 по оси ординат и 3/2 по оси абсцисс должна сов-
падать с кривой
τ τ
σ (ε ).
i
i
Считая кривую
τ τ
σ (ε )
i
i
опорной, можно постро-
ить зависимости
σ ) (ε
i
i
для некоторых видов напряженного состояния.
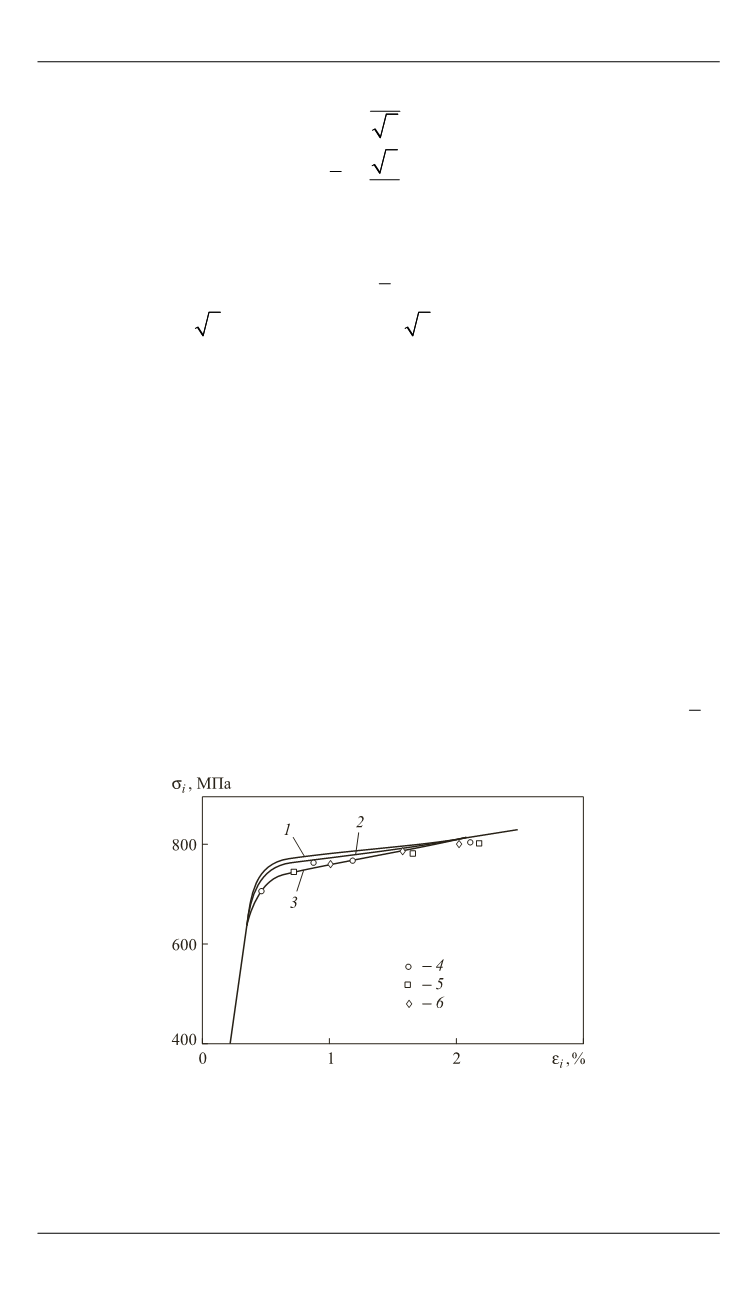
На рис. 1 в координатах
σ
i
—
ε
i
изображены результаты испыта-
ний трубчатых образцов, выполненных из стали ЭИ415 [3], при раз-
личных отношениях осевого напряжения
σ
z
к окружному
σ
t
. По опор-
ной кривой, соответствующей одноосному растяжению (см. рис. 1, кри-
вая
2
) были построены две кривые, соответствующие чистому сдвигу
(кривая
1
) и
σ 1 /σ
z t
(кривая
3
). Расположение экспериментальных то-
чек отвечает следствию, вытекающему из предлагаемой нами схемы
деформирования, — кривые
σ ) (ε
i
i
для
σ
1 / σ
z
t
располагаются ниже,
а для
σ / σ 0
z
t
выше, чем кривая
2
. Обработка результатов аналогич-
ных экспериментов на металлах при двухосном напряженном состоя-
нии [4] показала, что гипотеза о существовании единой кривой
)ε(
i
i
p
выполняется лучше, чем
σ ) (ε .
i
i
Рис. 1.
Пластическое деформирование трубчатых образцов
из стали ЭИ415:
1
— чистый сдвиг;
2
— одноосное растяжение;
3
—
σ
;
/ σ 1
z
t
4
–
6
—
σ / σ 0,5; 0, 25; 0, 75
z
t
соответственно


