Метод контрольного объема для расчета гидравлических сетей
3
тодов являются необходимость хорошего начального приближения и
низкая скорость сходимости.
Этих недостатков лишен градиентный метод (Global Gradient
Algorithm, GGA), предложенный Эзио Тодини в 1987 г. [2]. Данный
алгоритм сочетает в себе быструю сходимость и высокую точность
решения. Наиболее полно описание градиентного метода изложено
в руководстве пользователя программного комплекса EPANET,
написанного Льюисом Россманом [7].
Однако для гидравлических сетей со сложной топологией и со-
противлениями участков контура, отличающимися более чем на
10 порядков, используемые методы не обеспечивают сходимости
итерационного процесса, особенно для сетей, на которых установле-
ны регуляторы расхода или давления [3, 8]. Поэтому авторами пред-
ложен новый метод численного моделирования гидравлических сетей
со сложной топологией, основанный на дискретизации уравнения не-
разрывности. Данный метод аналогичен методу расчета гидравличе-
ских сетей при помощи метода конечных элементов и описанного
в работах [9, 10].
Постановка задачи.
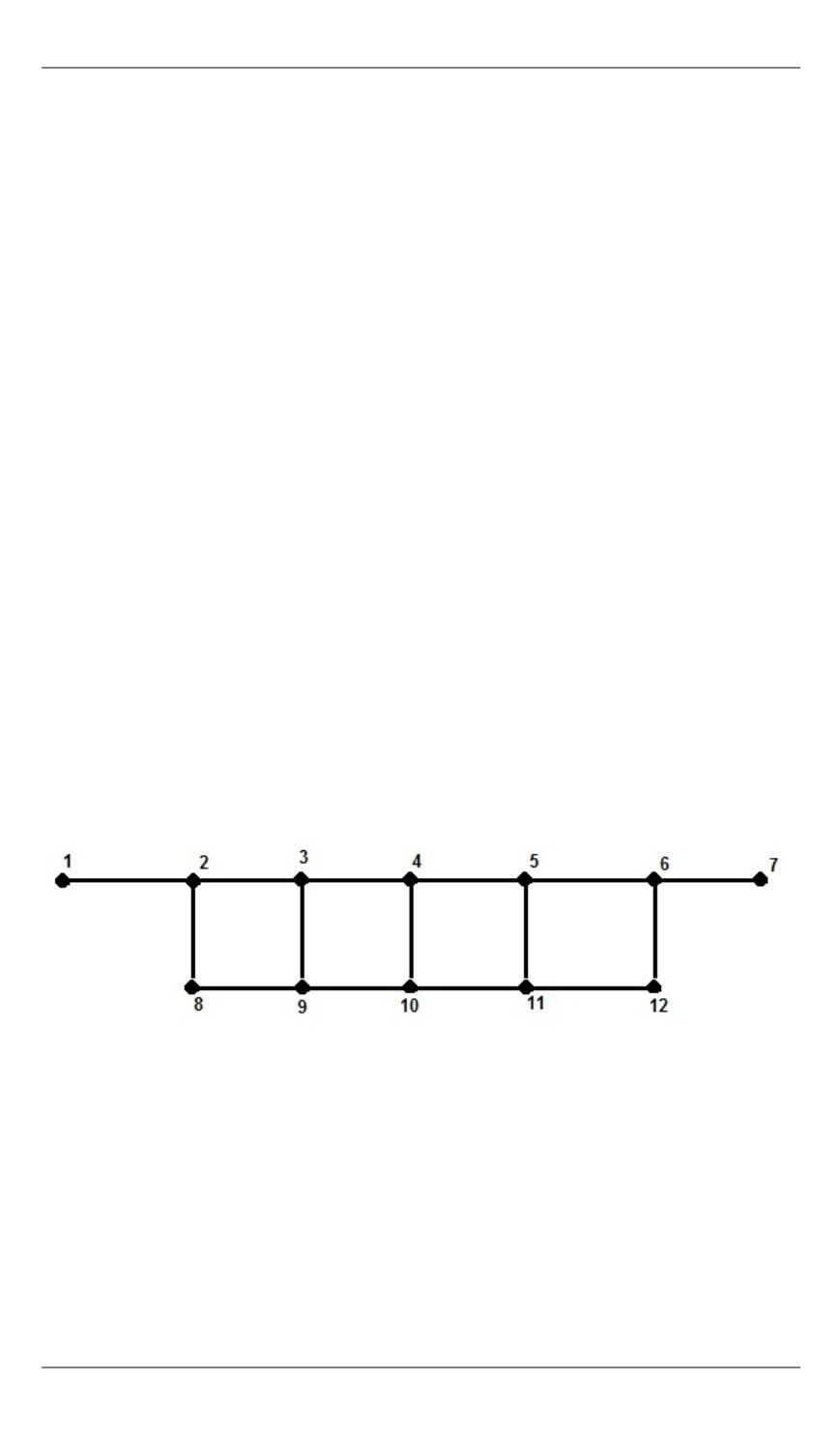
Рассмотрим постановку задачи потокорас-
пределения для гидравлической сети, показанной на рис. 1. Гидрав-
лическая сеть состоит из гидравлических связей, которые представ-
ляют собой каналы (трубы) заданной длины с постоянной площадью
сечения, и узлов, в которых происходит объединение гидравлических
связей.
Рис. 1.
Схема гидравлической сети
На рис. 1 узлы отмечены цифрами и показаны в виде ромбов,
а гидравлические связи представляют собой отрезки между узлами.
При этом значения давления и источники массы задаются только
в узлах, а коэффициенты гидравлического сопротивления и гидрав-
лического трения — только для гидравлических связей.
Математическая модель.
Движение жидкости в гидравлической
сети считается стационарным и изотермическим. Тогда в общем слу-
чае описание изотермического движения жидкости происходит при


