О.В. Белова, В.Ю. Волков, А.П. Скибин
10
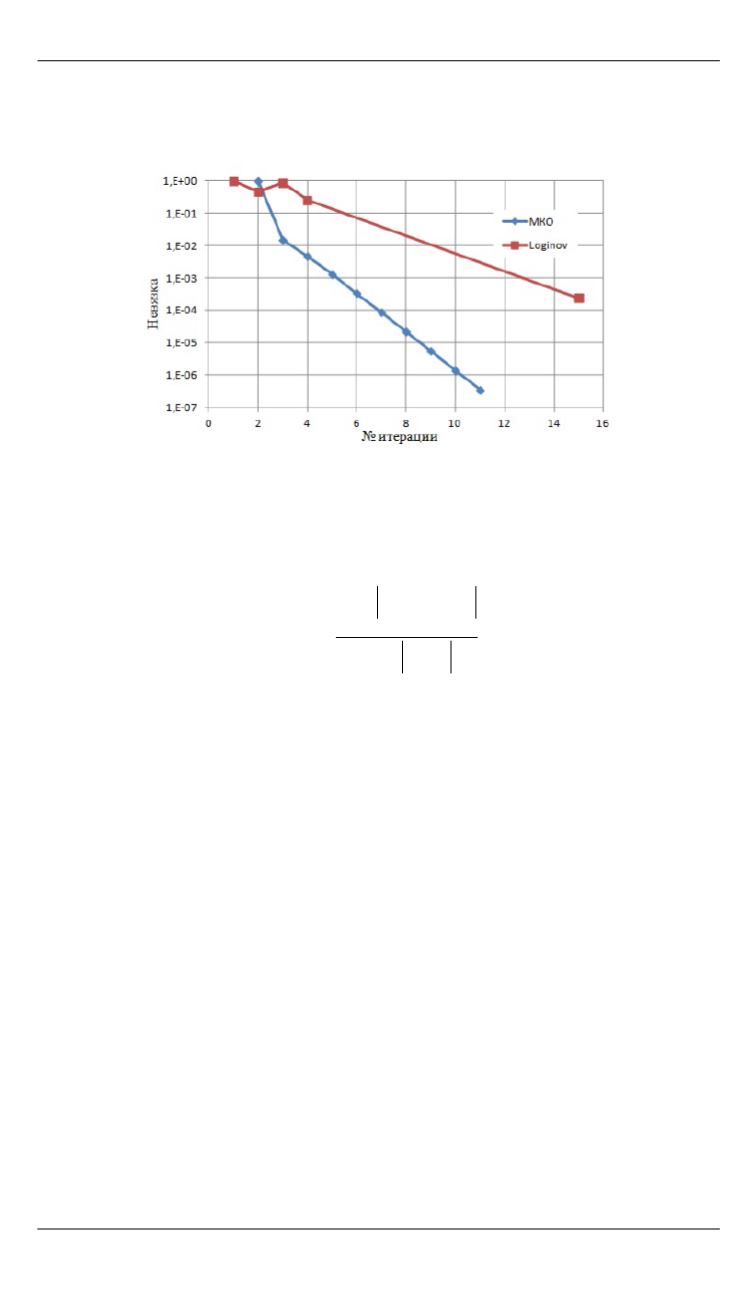
Авторами проведено исследование скорости сходимости задачи
от числа итераций. Изменение невязки по итерациям представлено
на рис. 4.
Рис. 4.
Скорость сходимости: МКО — метод контрольного объема;
Loginov — данные статьи [14]
Для определения невязки
использовалось следующее выра-
жение:
1
1,
1
1
1,
Φ
,
m m
i
i
i N
m
m
i
i N
Q Q
Q
где
m
i
Q
— объемный расход на
i
-м элементе расчетной схемы на
m
-й
итерации, м
3
/с.
Как видно из рисунка, скорость сходимости предлагаемого мето-
да контрольного объема выше по сравнению с вариантом метода
контурных расходов Андрияшева—Лобачева—Кросса, применямого
в [14]. При этом можно отметить, что при численном решении
с помощью МКО невязка уменьшается монотонно, тогда как для
«увязочных» методов сходимость задачи является немонотонной.
В качестве другой тестовой задачи для проверки работоспособ-
ности предложенного метода контрольного объема была рассмотрена
тестовая задача из статьи [15], описывающая потокораспределение
в гидравлической сети, с коэффициентами трения, являющимися
функцией числа Рейнольдса. Топология расчетной области представ-
лена на рис. 5. Гидравлическая сеть состоит из 18 связей, номера ко-
торых показаны на рис. 5 в середине каждой связи, и 13 узлов, номе-
ра которых также приводятся на рис. 5. В узле
1
задан постоянный
напор, схематически изображенный на рис. 5. В результате гидравли-
ческого расчета требуется определить напор в узлах сети. Полная по-
становка данной задачи приводится в [15], где также приводится об-


