Л.Г. Ветров, А.Л. Сунчалина
4
размера с распределением
0;1
R
(функция «Случайное число») и
вычислив значения этих оценок, можно сделать вывод об их эффек-
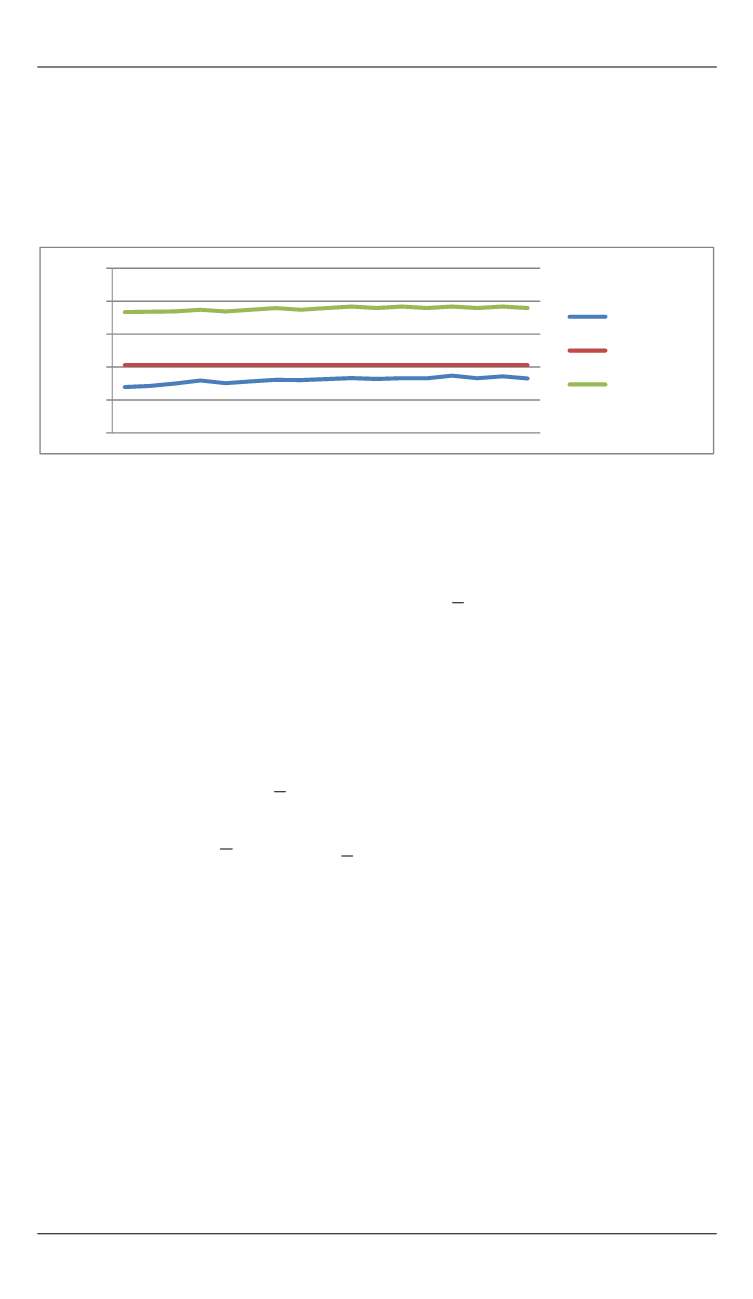
тивности по близости значений оценок к 1. На рис. 3 представлена
типичная картина зависимости этих трех оценок от объема выборки
(объем выборки порядка 2000).
Рис. 3.
Сравнение оценок
2. Построение доверительных интервалов и проверка стати-
стических гипотез.
При построении доверительных интервалов для
параметров основных параметрических моделей обычно достаточно
рассчитать выборочные характеристики
2
;
X S
и квантили соответ-
ствующих распределений статистик. Все это содержится в наборе
функций Excel, и задача построения доверительных интервалов сво-
дится к очень простым вычислениям. Единственное, на что следует
обратить внимание студентов, — это то, что среди функций Excel
имеется две функции дисперсии: «ДИСПР» — обычная выборочная
дисперсия
2
2
1
/
n
i
i
S
x x n
и «ДИСП» — «исправленная» выбо-
рочная дисперсия
2
2
1
/ ( 1).
n
i
i
S
x x n
В «Пакете анализа» для проверки гипотез есть ряд критериев, но
студент должен учитывать два момента: а) все эти критерии имеют от-
ношение к нормальному (гауссов) распределению; б) это критерии од-
нородности, т. е. сравниваются средние значения или дисперсии двух
выборок. Поэтому при использовании этих критериев для негауссовых
распределений они не гарантируют заданную вероятность ошибки пер-
вого рода, а для проверки простой гипотезы о среднем или дисперсии
границы критической области следует вычислять с помощью функций
Excel. Еще одна особенность программ проверки гипотез в «Пакете
анализа» — это альтернативные гипотезы: односторонние критические
значения можно использовать при проверке основной гипотезы
0 1
2
:
H a a
при альтернативе
1 1
2
:
H a a
. Для того чтобы разобраться
0,99
0,995
1
1,005
1,01
1,015
Среднее
Максимум
Медиана


