Лабораторные работы в курсе математической статистики
3
(например, зарплата жителей региона), то оценка среднего генеральной
совокупности с помощью выборочного среднего может оказаться не-
эффективной.
Вторая задача лабораторной работы демонстрирует возможности
методов статистического моделирования при сравнении эффективно-
сти различных несмещенных оценок параметров. Известно, что эф-
фективность несмещенных оценок характеризуется их дисперсией:
чем меньше дисперсия, тем оценка лучше.
Для модели равномерного распределения
0;
R
предлагается
сравнить три несмещенные оценки:
1
2
X
(метод моментов),
2
1
n
n X
n
(скорректированная оценка метода максимального
правдоподобия) и
3
/2
2
n
X
(удвоенная выборочная медиана).
Для
1
дисперсия считается легко, с несколько большими труд-
ностями можно посчитать дисперсию
2
, а вот для
3
это сделать
значительно сложнее. Смоделировав выборку достаточно большого
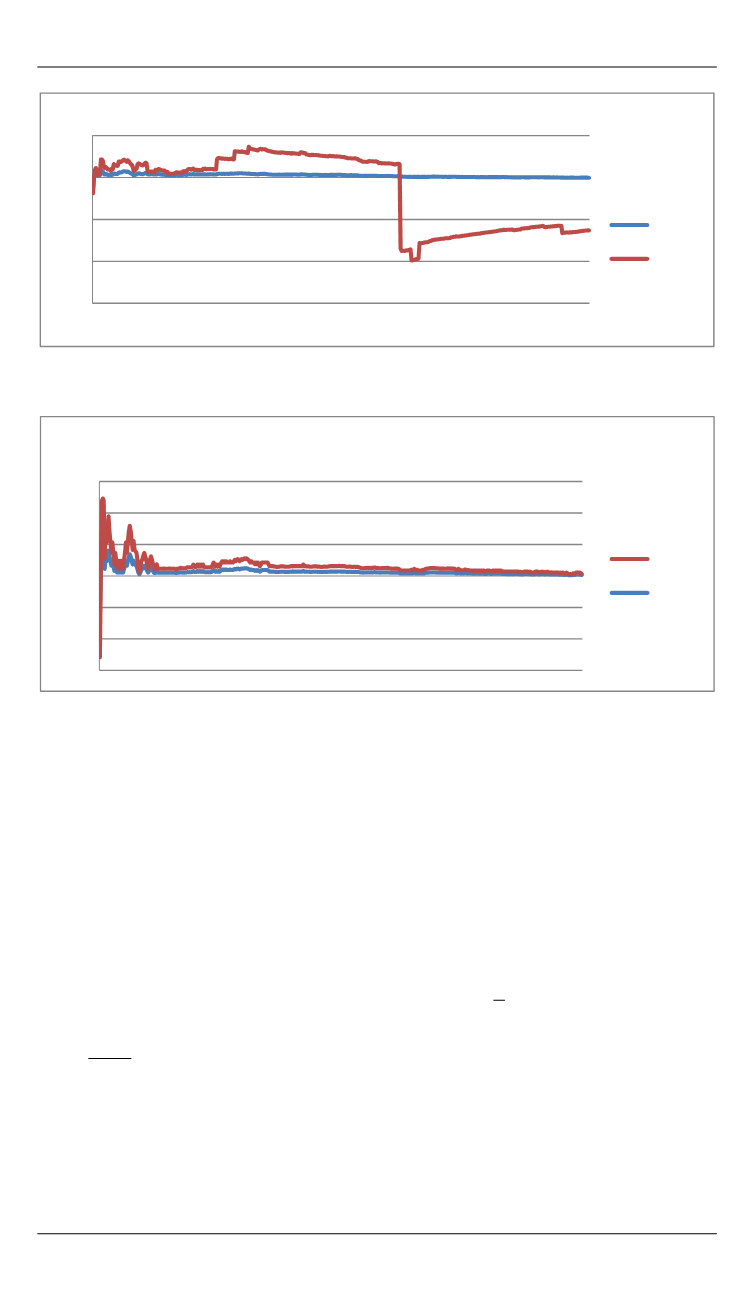
Рис. 1.
График зависимости выборочного среднего от объема выборки
‐1,5
‐1
‐0,5
0
0,5
1
1,5
1
25
49
73
97
121
145
169
193
217
241
265
289
313
337
361
385
409
433
457
481
Выборочные медианы
Коши
Гаусс
Рис. 2.
График зависимости выборочной медианы от объема выборки
‐6
‐4
‐2
0
2
1
25
49
73
97
121
145
169
193
217
241
265
289
313
337
361
385
409
433
457
481
Выборочное среднее
Гаусс
Коши


