А.А. Гурченков, А.М. Романенков
10
проходом. При обратном проходе необходимо выбирать новое управ-
ление. На каждой итерации управление следует выбирать так, чтобы
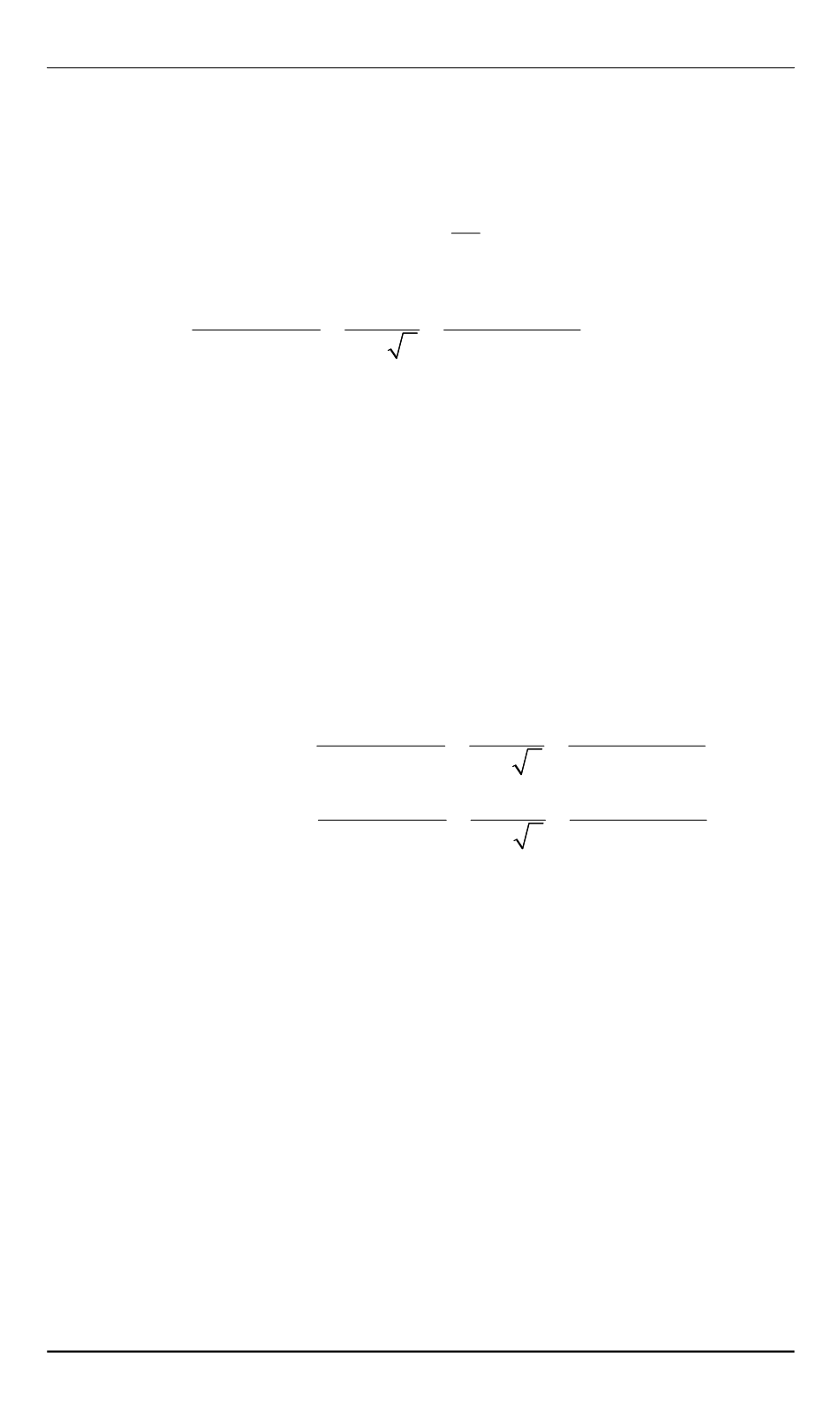
функция Гамильтона была максимальной по управлению, т. е.
min
max
7
6
2
, ,
2
max
min
x y z
x
y
u u u u u
u t
H
u u
6 01
7 10
8 11
9 02
10 20
ch
ch2
ch 2
,
z
q
q
q
q
q u D
где
D
— слагаемые функции Гамильтона, которые не зависят от
управлений.
В силу того, что управления линейно входят в функцию Гамиль-
тона (9), поиск оптимального управления достаточно прост:
min
7
max
7
min
6
max
6
6 01
7 10
8 11
9 02
10 20
min
6 01
7 10
8 11
9 02
10 20
max
, если
0;
, если
0;
, если
0;
, если
0;
, если
0;
ch
ch2
ch 2
, если
ch
ch2
ch 2
x
y
z
u
u
u
u
u
u
u
q
q
q
q
q
u
u
q
q
q
q
q
u
0.
(12)
Ниже приведены численные тесты и результаты вычислений для
различных возмущений. На рис. 1
рассмотрены симметричные возму-
щения. В начальный момент времени
02
0.
q
Численный эксперимент
показывает, что асимметричные гармоники не возбуждаются.
На рис. 2 представлено оптимальное управление в виде кусочно-
постоянной функции. Отметим, что для гашения симметричных ко-
лебаний используется только сила, направленная вдоль вертикальной
оси.
На рис. 3 показана асимметричная гармоника
01
0.
q
Видно, что
возникают и симметричные возмущения
02
(
0).
q
Асимметричные колебания невозможно погасить, действуя только
вертикальной силой (рис. 4). Вектор управления содержит все компо-
ненты.


