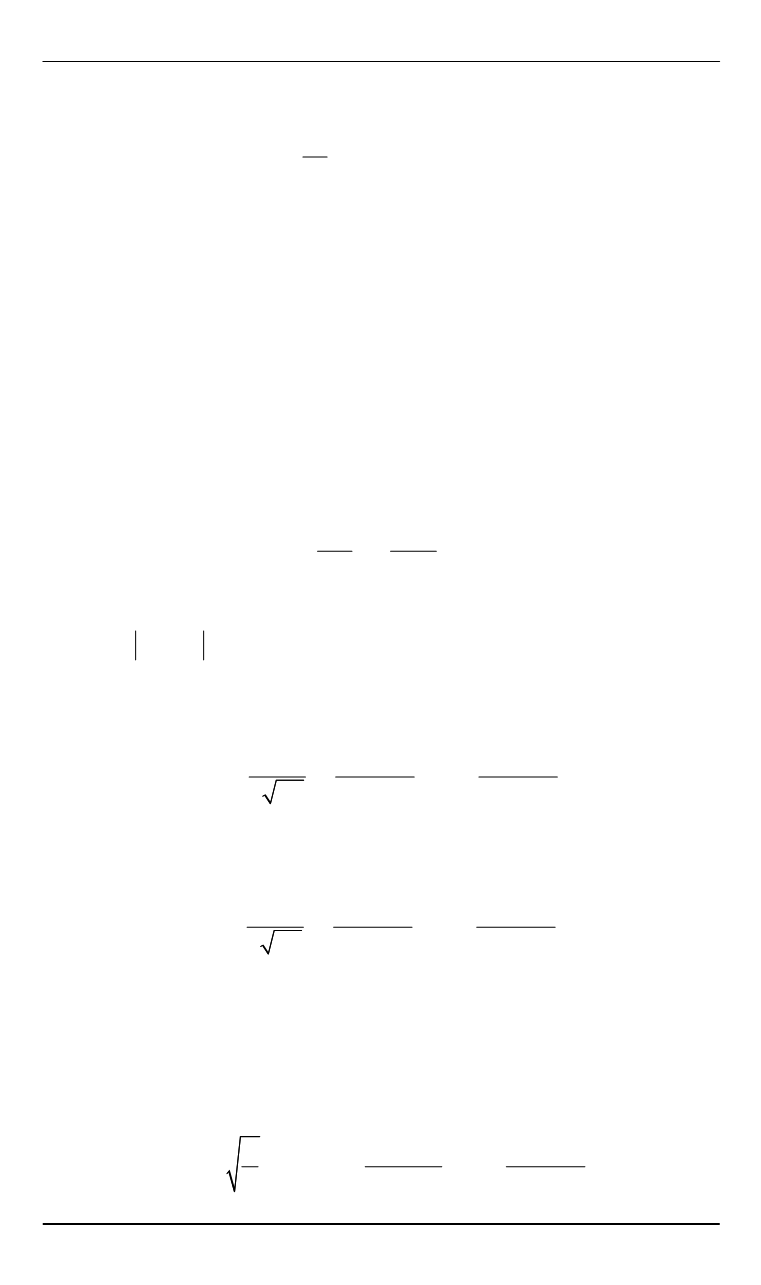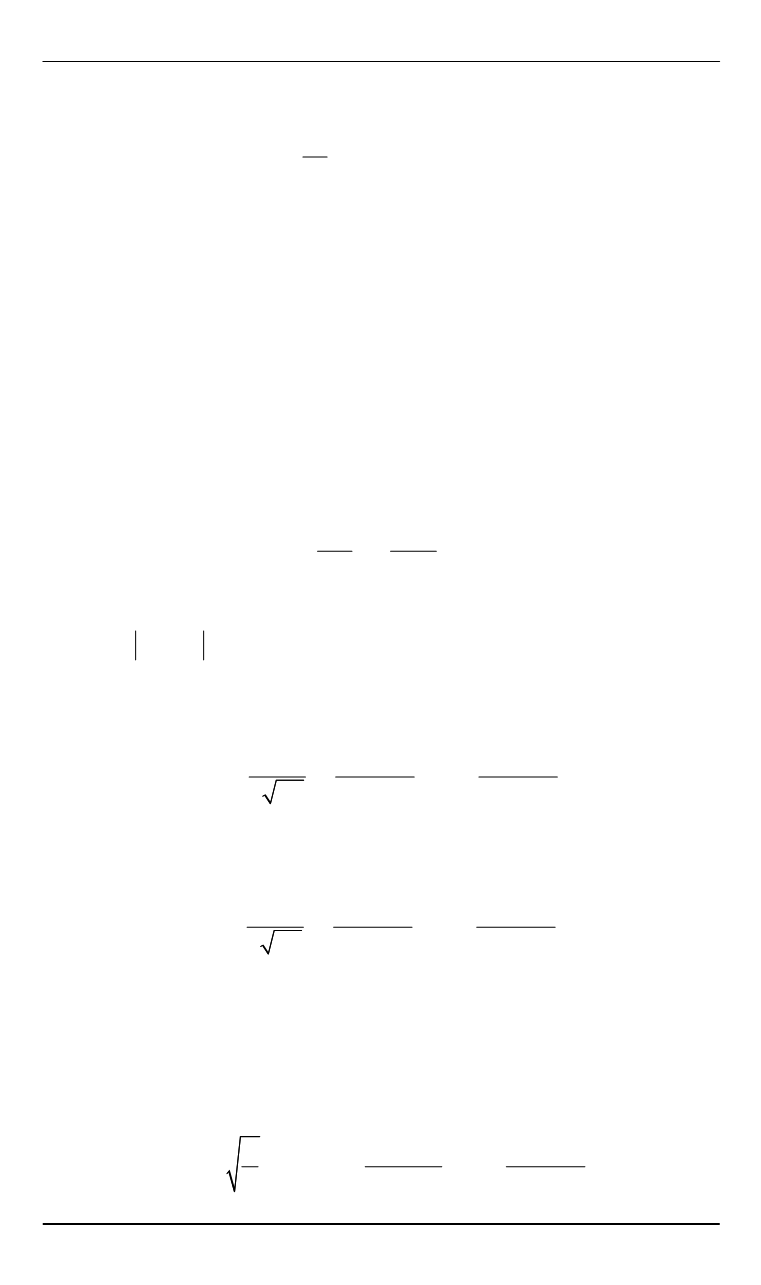
А.А. Гурченков
4
где
0
,
y
e
и
0
2 (
),
( , ) 0,
,
0.
y
q V e
y
q y t
y
t
(4)
При этом поле скоростей определяется из уравнений (3), а поле
давлений — из уравнений (4) по найденному полю скоростей.
Решение системы (3) ищем в форме
( , )
( , ) sin 2
( , )
cos 2 ;
( , )
( , )
( , ) ,
y
x
x
z
z
V y t W y t
t W y t e
t
W y t W y t e W y t e
(5)
где
( , )
W y t
— неизвестная функция.
Подставляя соотношения (5) в (3), получаем для определения
W
следующую задачу:
2
2
;
(0, ) ( ) sin 2
( ) ( )
cos 2 ,
0;
( , ) 0,
,
0,
( , 0) 0,
0.
y
W W
t
y
W t u t
t u t u t e
t t
W y t
y
t
W y
y
(6)
Решение уравнений (6) представляет собой известное выраже-
ние [10]
2
3/2
0
(0, )
( , )
exp
.
4 (
)
(
)
2
t
y
W
y
W y t
d
t
t
(7)
Используя формулу (7), из уравнений (5) находим поле скоростей
жидкости в виде
2
3/2
0
( , )
( , )
exp
.
4 (
)
(
)
2
t
y
T t
y
V y t
d
t
t
(8)
Здесь
( , ) ( ) cos 2 (
) ( )
sin 2 (
).
y
T t u
t
u e
t
(9)
Решая уравнения (4) с правой частью, полученной с учетом вы-
ражений (8), (9), находим поле давлений
2
0
1/2
0
( , )
( , ) 2 (
)
exp
.
4 (
)
(
)
t
y
T t
y
q y t
e
d
t
t
(10)