
Возмущение температурного поля трещиной в полимерных материалах
Инженерный журнал: наука и инновации
# 11·2017 3
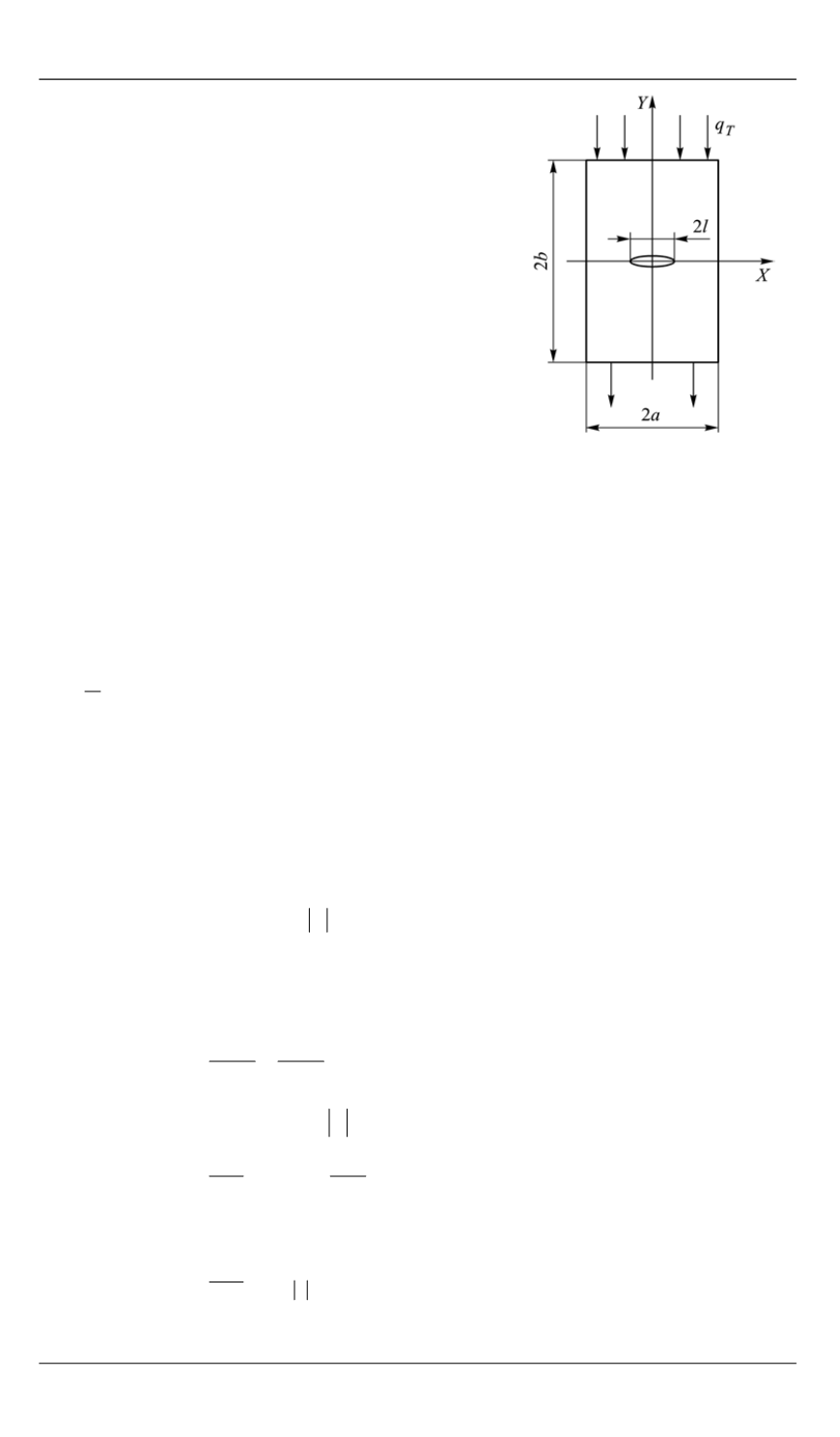
Рис. 1.
К задаче о темпера-
турном поле образца с тре-
щиной
В начале процесса, когда подача тепла
только началась, в образце возникает
нестационарное распределение темпера-
туры. С течением времени переходные про-
цессы затухают и устанавливается стацио-
нарное распределение, не зависящее от
времени. Такое стационарное состояние и
будет рассматриваться.
Анализ экспериментальных данных
показывает [8], что внутренние микро-
трещины в полимерах и композитах на их
основе имеют начальные размеры порядка
0,03…0,3 мкм, критический предраз-
рывный размер трещины примерно в 6–10
раз больше, т. е. также весьма мал. В
качестве примера рассмотрим образец-
полоску полиметилметакрилата (ПММА) длиной 2
b
= 20 мм и
шириной 2
а
= 5 мм (это типичные размеры образцов, используемых
при испытаниях на долговечность). Начальная трещина в ПММА
имеет размер порядка
l
0
= 0,23 мкм [8]. Для такого образца
0, 25;
= =
a x
b
критическая предразрывная длина трещины может
достигать шести-десяти начальных размеров, т. е.
кр
1, 4...2, 3
l
мкм.
В любом случае размер трещины мал по сравнению с размерами
образца. Искажение температурного поля, вызванное такой трещиной,
сосредоточенно в малой ее окрестности. Все это позволяет в
соответствии с известным принципом микроскопа принять в качестве
математической модели рассматриваемой проблемы упругую плоскость
с разрезом вдоль отрезка
,
0,
≤ =
x l y
моделирующим трещину.
В такой постановке задача о стационарном распределении
температуры в образце с трещиной имеет следующий вид:
( )
2
2
2
2
2
0,
0;
,
\
,
0;
|
( — коэффициент теплопроводности);
|
0.
T
y
T
T
y x l
T T
x
y
x y R x l y
T
q
y
T
y
→±∞
= <
∂ ∂+ =
∂ ∂
∈ < =
∂
=
∂
λ
λ
∂
=
∂
(1)
















