
Лан Аньци
6
Инженерный журнал: наука и инновации
# 7·2017
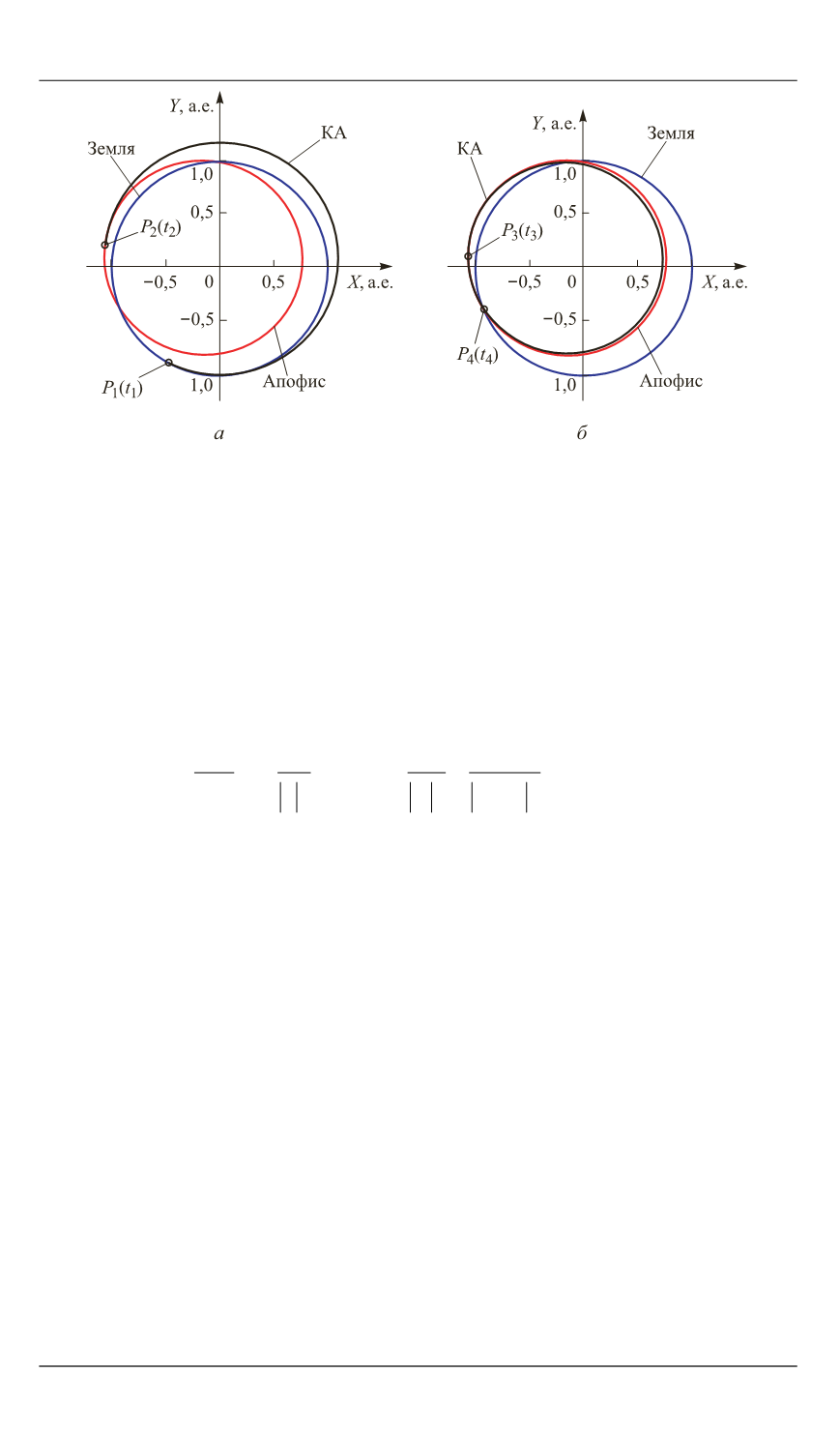
Рис. 2
. Межпланетные перелеты КА для второго случая, когда на некотором гелио-
центрическом участке есть один пассивный виток
u
б
> 2π:
а
— от Земли (
P
1
) до Апофиса (
P
2
);
б
— от Апофиса (
P
3
) до Земли (
P
4
)
Уточненный расчет оптимальных траекторий выполняется чис-
ленным решением системы дифференциальных уравнений движения
КА с учетом притяжения Земли (с учетом ее сжатия), Луны, Солнца,
планет и давления солнечного света:
2
E
2
3
3
3
,
i
i
i
i
i
i
d
dt
r
r r r
r
Δ
r
r r r
(5)
где
r
(
x, y, z
) — радиус-вектор КА в прямоугольной невращающейся
геоцентрической системе координат;
r
i
— радиус-вектор
i
-го небес-
ного тела; μ
E
и μ
i
— гравитационные параметры Земли и
i
-го небес-
ного тела;
— ускорение вследствие сжатия Земли.
Уравнение (5) интегрируется на два пассивных участка полета:
первый — от начального момента пассивного полета после разгона
КА вблизи Земли,
t
in
=
t
0
p
(
t
0
p
<
t
1
), до конечного времени полета КА к
Апофису,
t
f
=
t
2
; второй — от момента после разгона КА вблизи асте-
роида,
t
in
=
t
3
, до момента входа КА в сферу действия Земли,
t
f
=
t
4
.
С учетом ограничений на расстояния от КА до астероида или до Земли
в концах этих участков полета для сращивания решаются краевые зада-
чи варьированием начальных данных. Так, для траектории
P
1
с
u
< 2π
начальное время
t
0
p
на основе решения задачи Ламберта получилось
равным 2021,1,20,10:17:32. После коррекции
t
0
p
уменьшилось на 5 мин.
Для траектории
P
2
с
u
> 2π сначала
t
0
p
составило 2019,5,19,15:37:24.14,
после коррекции оно увеличилось на 1 мин 21 с.
















