
С.А. Заборский, Е.В. Кирилюк
6
Инженерный журнал: наука и инновации
# 5·2017
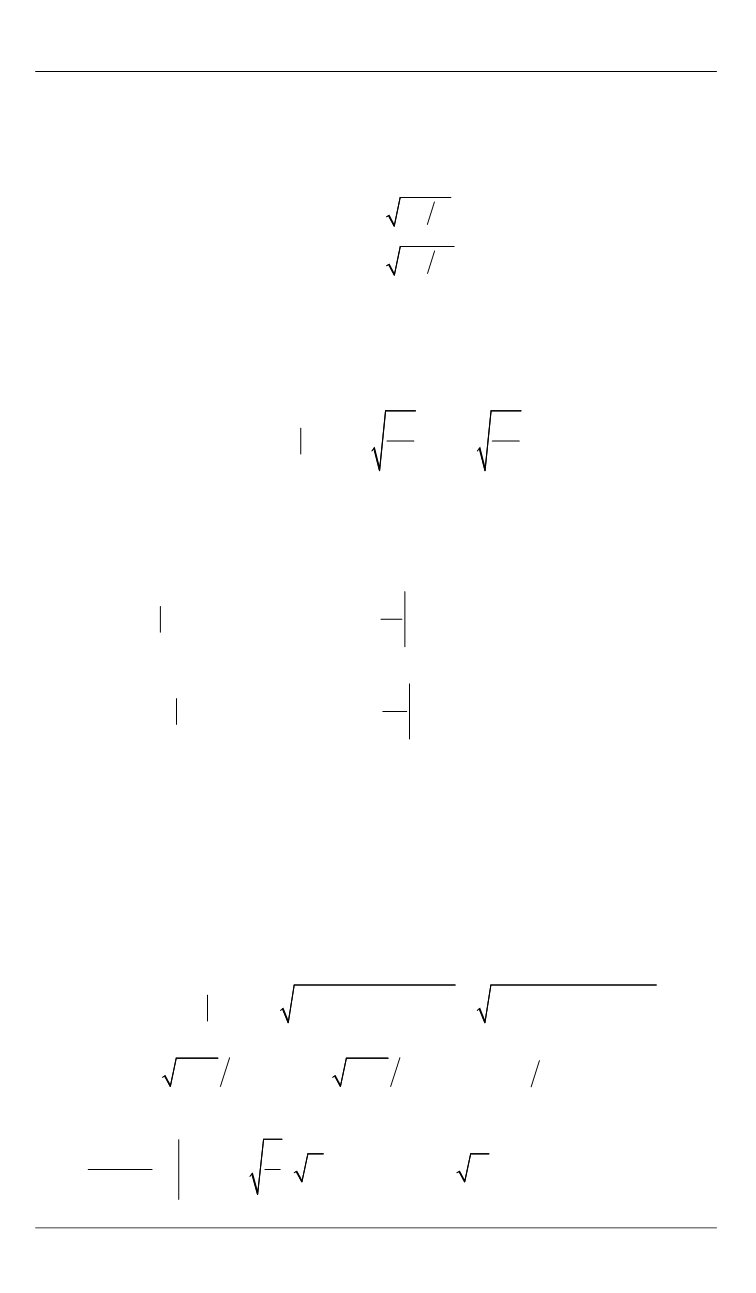
Рассмотрим еще один частный случай. При стремлении радиуса
апогея переходных орбит к бесконечности
(
)
r
α
→ ∞
получаем:
1
2
0
H H
v
v
α
α
= =
,
1
1
2
H
v
r
= µ
,
2
2
2 ,
H
v
r
= µ
т. е. переходные орбиты становятся параболическими, и биэллипти-
ческий переход вырождается в бипараболический. Суммарное им-
пульсное приращение скорости при бипараболическом переходе со-
ставит
III
0
3
1
2
2
2 .
r
v
v
v
v
r
r
α
∞Σ
Σ →∞
µ
µ
∆ = ∆
= − + −
(12)
Обозначим углы наклона вектора скорости к местному горизонту
в соответствующих
i
-х точках
.
i
γ
Тогда из выражений (6)–(9) с уче-
том принятого обозначения, также следует, что при
r
α
→ ∞
2
1
1
0
2 cos ,
r
p
r
α→∞
=
γ
1
1
0
tg
ctg ctg ;
2
r
α→∞
θ
= γ = γ
(13)
2
2
2
3
2 cos ,
r
p
r
α→∞
=
γ
2
2
3
tg
ctg ctg .
2
r
α→∞
θ
= γ = γ
(14)
Следовательно, биэллиптический переход является котангенци-
альным, т. е. осуществляется импульсами, направленными вдоль век-
торов скорости в точках их приложения, при этом угловая дальность
между точками приложения импульсов не кратна
.
π
Определим условие, описывающее 2-ю границу оптимальности
трехимпульсного решения задачи. Суммарное импульсное прираще-
ние скорости при двухимпульсном перелете между точками на эл-
липтических орбитах составляет [5]
(
)
(
)
2
2
2
2
II
III
3
3 1
0
0
2
0
.
r
H
r
H
v
v
v
v v v
v v v
α
Σ
Σ
θ
θ
θ
θ
∆ =
∆ = ∆
= + +
− + +
(15)
Здесь
1
1
H
H
v
p r
θ
= µ
,
2
2
H
H
v
p r
θ
= µ
,
(
)
1 2 1 2
2
H
p r r r r
=
+
.
Если
II
v
v
∞Σ
Σ
∆ = ∆
и выполняется условие
(
)
(
)
(
)
2 III
1
1
2
2
1 2cos
1 2cos
0,
2
r
v r
r
r
r
α
Σ
α
α
→∞
∂∆
µ =
+ θ + − θ <
∂
(16)
















