
Оптимальный биэллиптический переход между компланарными эллиптическими орбитами
Инженерный журнал: наука и инновации
# 5·2017 3
Важно отметить, что углы
1
θ
,
2
θ
между точками приложения
импульсов скорости (между векторами
1
r
и
r
α
,
r
α
и
2
r
соответствен-
но) не являются фиксированными, т. е. направление вектора
r
α
не задано, а векторы
0
v
,
3
v
,
1
r
и
2
r
не являются фиксированными
в инерциальном пространстве. Таким образом, оси апсид начальной
и целевой эллиптических орбит, на которых расположены точки
P
и
Q
соответственно, могут вращаться в инерциальном пространстве.
Задача состоит в выборе таких двух переходных орбит с фикси-
рованным радиусом апогея
r
α
и таких направлений приложения им-
пульсов (направлений вектора тяги), характеризуемых углами
1
ϕ
и
2
ϕ
(рис. 2), чтобы суммарное импульсное приращение скорости
III
1
2
v
v
v
v
Σ
α
∆ = ∆ + ∆ + ∆
(1)
было минимальным.
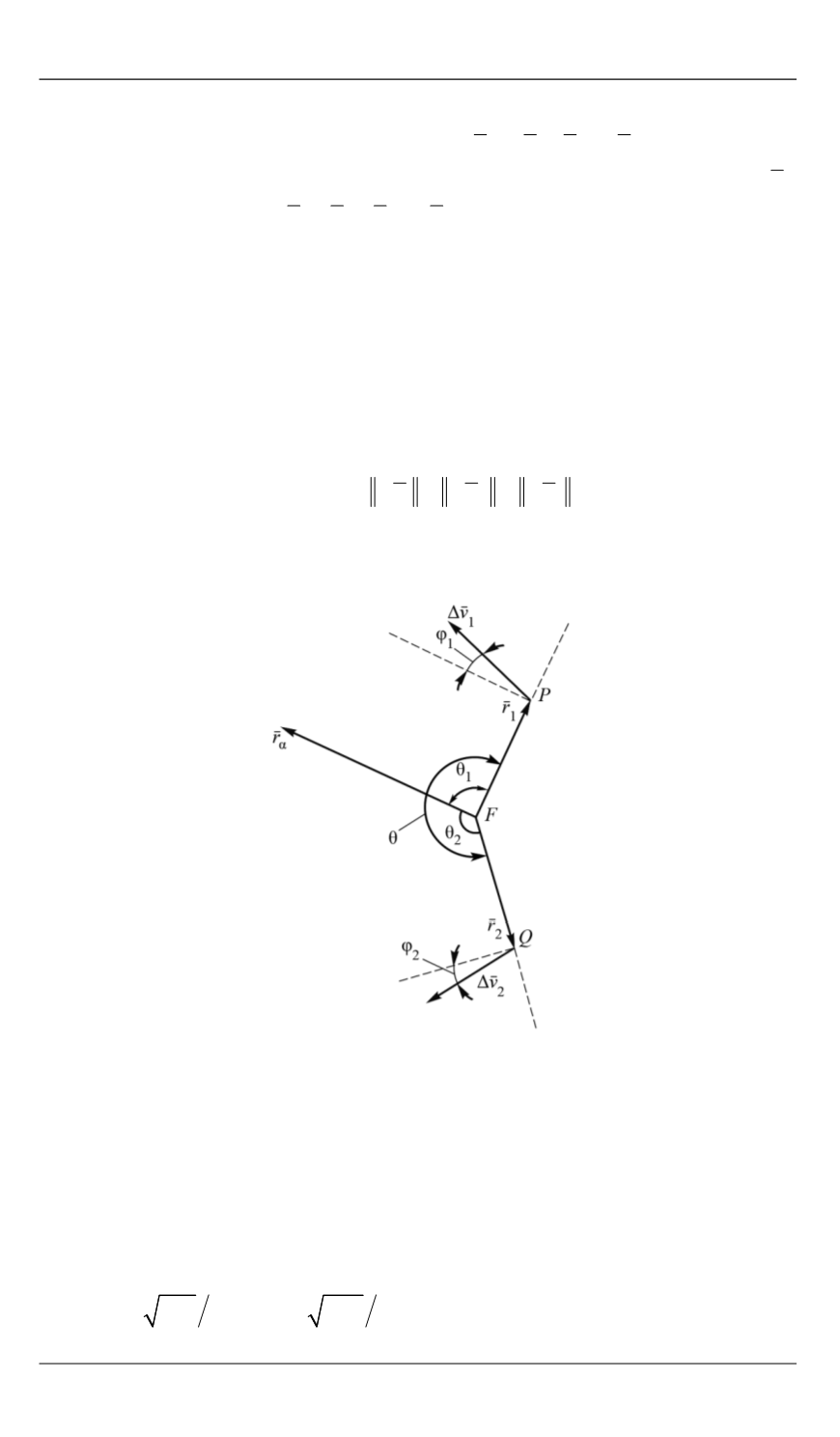
Рис. 2.
Схема направлений приложе-
ния импульсов скорости
Решение задачи биэллиптического перехода.
Импульс
v
α
∆
в
апогее 1-й переходной орбиты должен быть касательным, чтобы
сформировать апогей 2-й переходной орбиты. Его величина составит
2
1
,
v v v
α α α
∆ = −
(2)
где
1
1
,
v
p r
α
α
= µ
2
2
.
v
p r
α
α
= µ
















