Оптимальный биэллиптический переход между компланарными эллиптическими орбитами

5 / 13

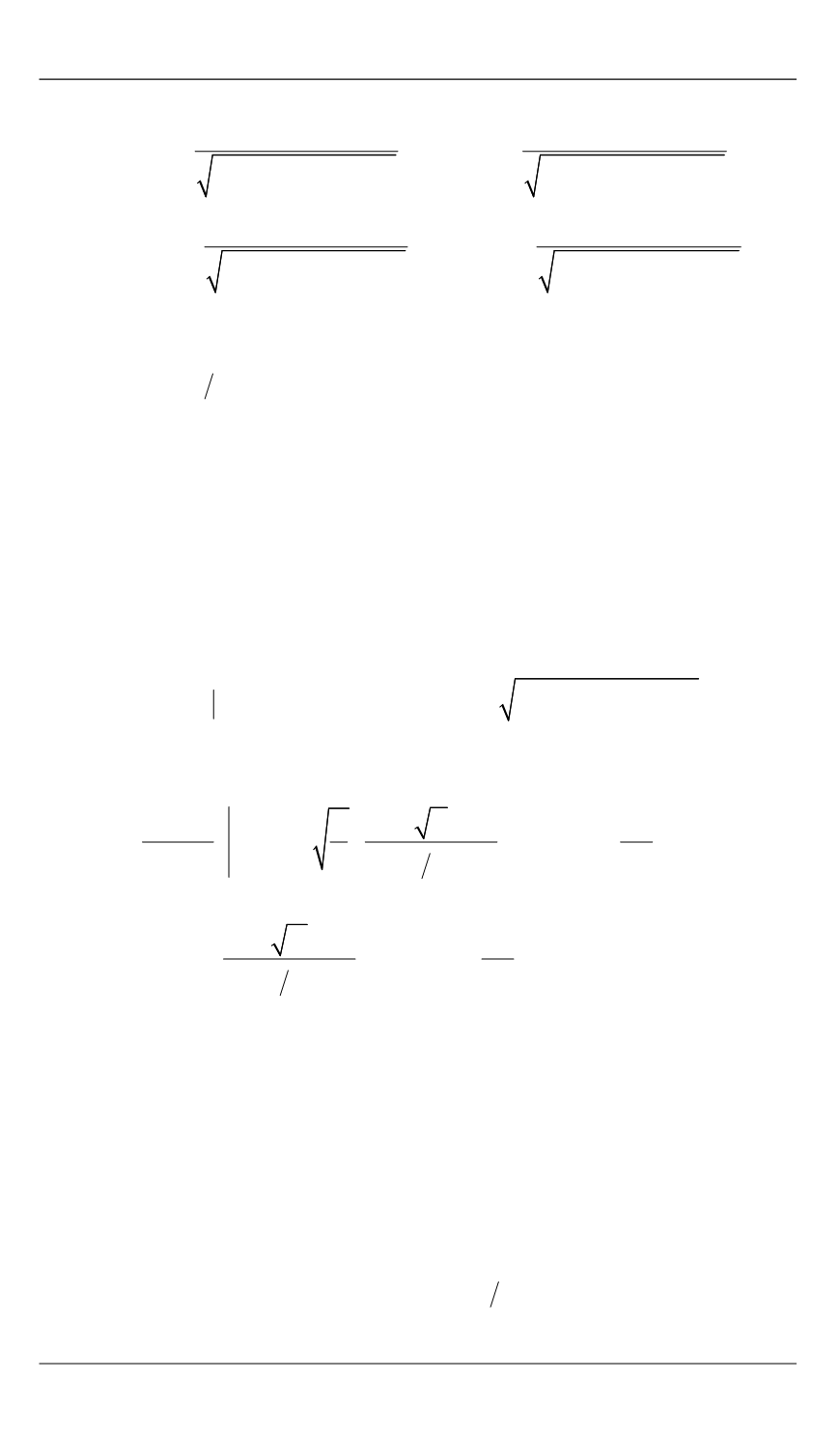
Оптимальный биэллиптический переход между компланарными эллиптическими орбитами
Инженерный журнал: наука и инновации # 5·2017 5
где
( )
0
1 2 2
0 0 1
sin r
r H
v
v v vn α
ϕ =
+ +
,
( )
3
2 2 2
3 3 2
sin r
r H
v
v v vn α
ϕ = −
+ −
; (8)
( )
0 1
1 2 2
0 0 1
cos H
r H
v v
v v v
θ α
θ α
+
ϕ =
+ +
,
( )
3 2
2 2 2
3 3 2
cos H
r H
v v
v v v
θ α
θ α
−
ϕ = −
+ −
. (9)
Анализ результатов. Трехимпульсный переход между точками
на эллиптических орбитах оптимален в зависимости от величины
отношения 3 r rα α (где 3 r α — радиус апогея целевой орбиты) и ис-
тинных аномалий граничных точек 0, ϑ 3. ϑ Проанализируем, при
каких условиях трехимпульсный переход будет энергетически вы-
годнее двухимпульсного.
В частном случае, когда радиус апогея переходных орбит rα ра-
вен радиусу апогея целевой орбиты 3 , r α биэллиптический переход
вырождается в двухимпульсный, для которого 2 0, v ∆ = 2-я переход-
ная орбита совпадает с конечной и суммарное импульсное прираще-
ние скорости составляет [5]
( )
3
2 2
III II 2 1 0 0 1 .
H r H
r r v v v v v v v
α α Σ Σα α θ α
= ∆ = ∆ = + − + + (10)
Тогда, если выполняется условие
( )
3
1 2 III 1
1
3/2
3
1 3
1 cos 2
2 1
r r
r v r
r
r r r r
α α
Σ
α
α α
α =
       ∂∆ µ =
+ ϕ + + 
     
 ∂      +
( )
2 2
2
3/2
3
1 3
1 cos 2 0,
1
r r
r r r α
α

   
+ + ϕ + <   
    + 
(11)
означающее, что с увеличением радиуса апогея rα (при 2 cos 0) ϕ <
величина суммарного импульса III v Σ ∆ должна уменьшаться, при
3 r rα α> биэллиптический перелет энергетически выгоднее двухим-
пульсного.
Исследование
3
III
( , )
min
r r
v
α α
Σ
∈ ∞
∆ для произвольных граничных орбит
представляет собой сложную задачу, решенную только для круго-
вых [7] и коаксиальных [8] граничных орбит. Для круговых гранич-
ных орбит условию (11) соответствует 2 1 15,58 r r > для соотношения
их радиусов [7].