
С.А. Заборский, Е.В. Кирилюк
2
Инженерный журнал: наука и инновации
# 5·2017
В настоящей статье исследован биэллиптический переход при за-
данной величине апогея переходных орбит с использованием данных
статьи [6], позволивших обобщить результаты, представленные в ра-
ботах [7, 8], для переходов между двумя определенными точками на
граничных несоосных эллиптических орбитах.
Постановка задачи.
Заданы геометрические характеристики
начальной и целевой эллиптических орбит: эксцентриситет и радиус
апогея. На начальной орбите истинной аномалией
0
ϑ
задана точка
,
P
которой соответствуют радиус-вектор
1
r
и вектор скорости
0
.
v
На
целевой орбите истинной аномалией
3
ϑ
задана точка
,
Q
которой со-
ответствуют радиус-вектор
2
r
и вектор скорости
3
.
v
Начальная и це-
левая орбиты лежат в одной плоскости (т. е. векторы
0
v
,
3
v
,
1
r
и
2
r
компланарны). Траектория перелета состоит из двух переходных ор-
бит с совпадающими апогеями, величина радиусов
r
α
которых зада-
на. Приложенный в точке
P
импульс
1 1 0
v v v
∆ = −
формирует 1-ю пе-
реходную орбиту. В апогее 1-й переходной орбиты прикладывается
такой касательный импульс
2
1
v v v
α α α
∆ = −
, чтобы 2-я переходная
орбита проходила через точку
.
Q
Суммарный импульс
1
v
v
α
∆ + ∆
перелета на 2-ю переходную орбиту должен быть при этом опти-
мальным (минимальным). Импульс
2 3 2
v v v
∆ = −
в точке
Q
2-й пере-
ходной орбиты изменяет модуль и направление вектора скорости для
получения требуемого
3
v
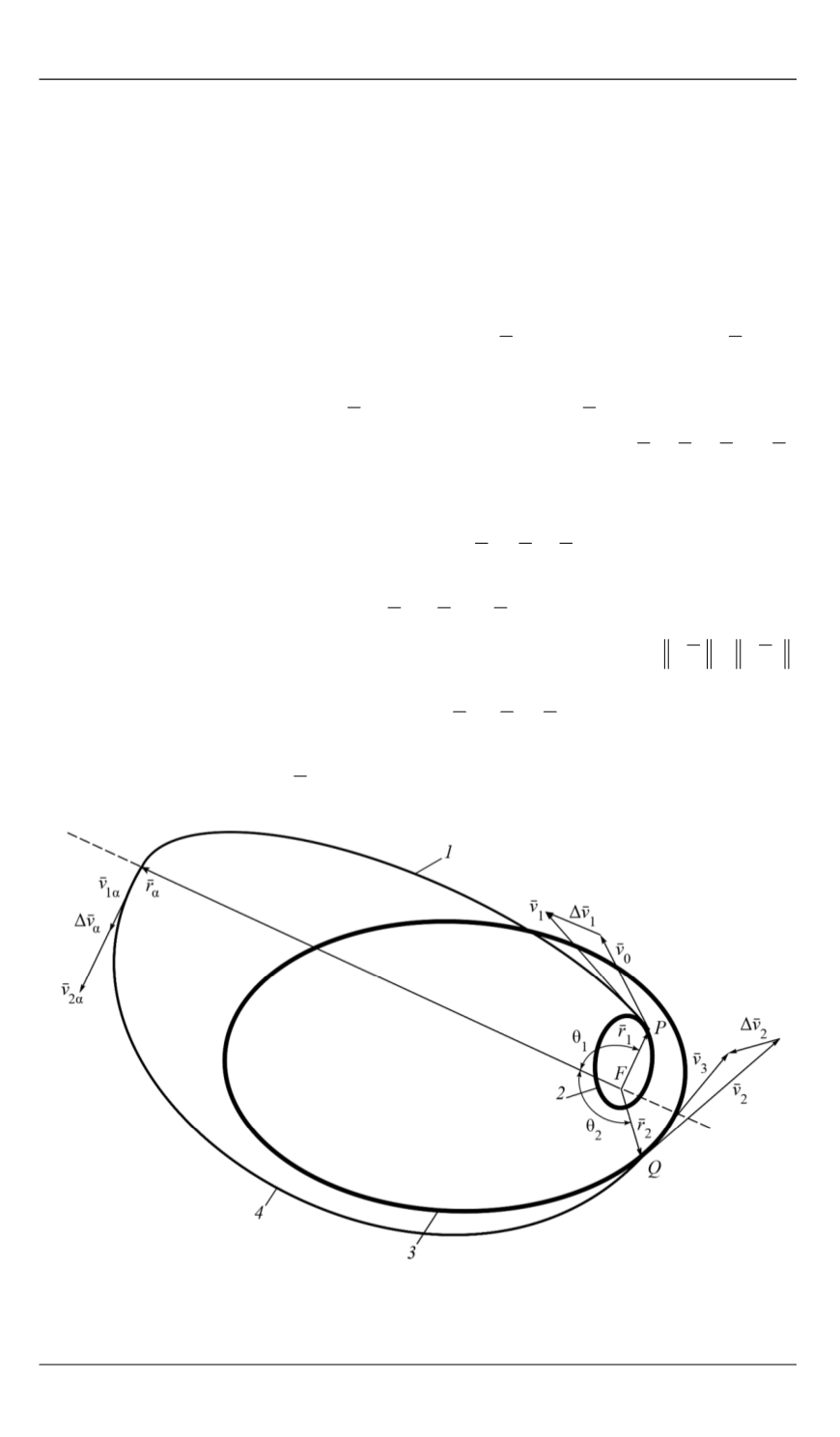
(рис. 1).
Рис. 1.
Схема биэллиптического перехода:
точка
F
— основной фокус, соответствующий положению притягивающего центра;
1
— 1-я пе-
реходная орбита;
2
— начальная орбита;
3
— целевая орбита;
4
— 2-я переходная орбита
















