
Л.К. Кузьмина
4
Инженерный журнал: наука и инновации
# 9·2016
УM
.
Ω × =
H M
С точки зрения механики это означает переход от исходной
задачи с
k
степенями свободы к упрощенной задаче (
k
У
— число сте-
пеней свободы;
k
У
=
N
У
/
2
;
k
У
<
k
) [2, 6, 16–18]. Но эти укороченные
модели — лишь формализованные математические абстракции, ко-
торые не описывают поведение никакого реального объекта [6];
в общем случае
k
У
— нецелое число [16]. Здесь имеет место матема-
тическая декомпозиция [8] для исходной системы. Такая ситуация
обусловливает специфические проблемы, актуальные как для теории,
так и для инженерной практики:
•
методология сведения к корректной модели меньшей размерно-
сти в динамическом анализе, включая сложные управляемые системы
[1, 3, 14, 19];
•
особый случай полной математической декомпозиции [6, 8]
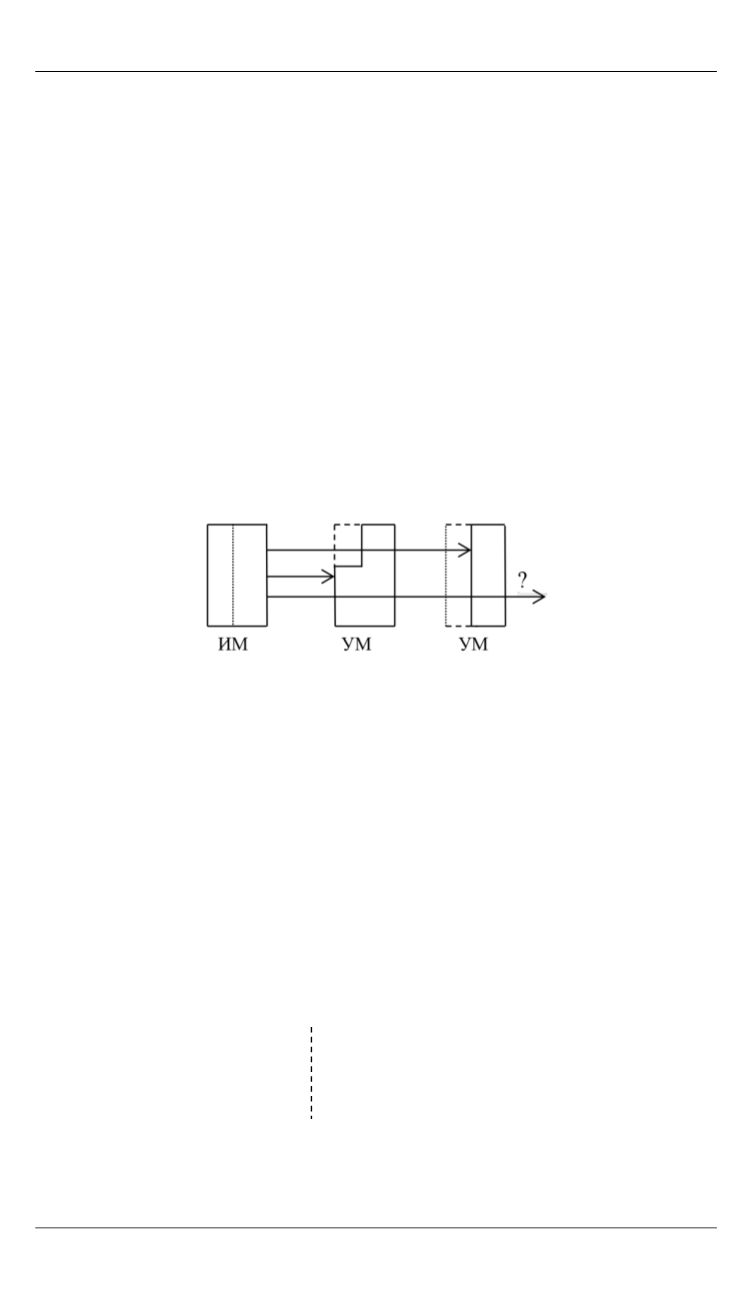
(см. рисунок).
Полная математическая декомпозиция
Сформулированные задачи очень важны в динамике систем ста-
билизации-ориентации с гироскопическими управляющими элемен-
тами, для которых имеют место критические особенные (в смысле
А.М. Ляпунова) случаи.
Рассмотрим систему одноосной гиростабилизации (ОГС) [7, 9, 19].
Пусть ОГС моделируется как механическая система с безынер-
ционным следящим приводом, где
H
— собственный кинетический
момент гироскопа;
q
= (
β
,
α
,
θ
);
β
— угол прецессии;
α
— угол ста-
билизации;
θ
— угол деформации оси подвеса гироскопа (принято, что
элементы подвеса гироскопа не обладают абсолютной жесткостью).
В данном случае ИM — это система вида:
ИM
1
...;
β − θ − α = − β +
A H H b
(4)
2
...;
α + θ + β = − α − β +
J B H b e
3
(
)
...,
θ ( α ( β = − θ − θ (
B
H b c
где
A
,
J
,
B
— соответствующие моменты инерции;
b
1
,
b
2
,
b
3
— соот-
ветствующие коэффициенты трения;
c
,
e
— коэффициенты обоб-


















