
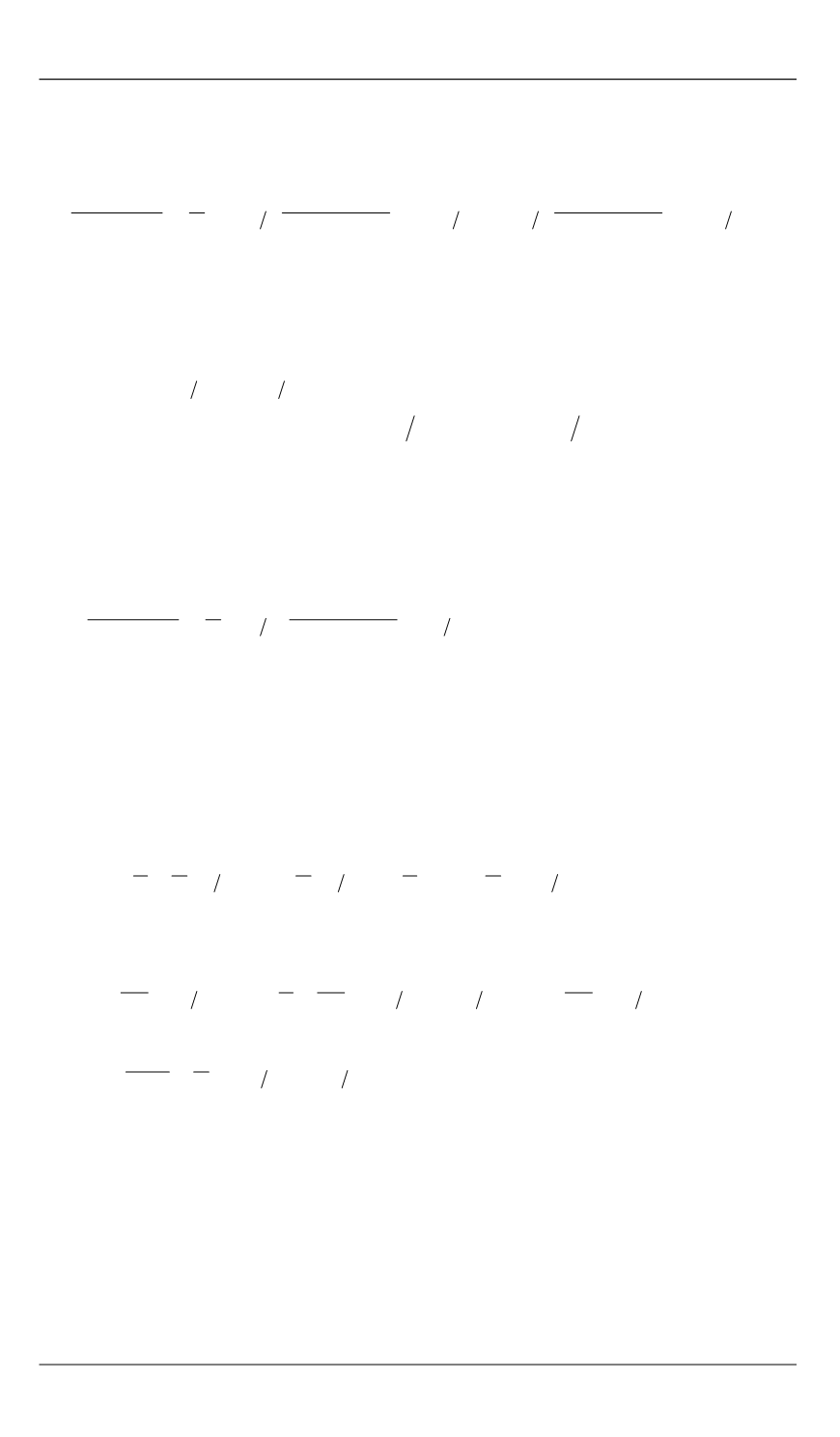
А.А. Гурченков, М.В. Носов
4
Инженерный журнал: наука и инновации
# 9·2016
Проведем конечно-разностную аппроксимацию прямой задачи
(1) по следующей схеме:
1
1
1
1
1
1
1
1
1
1
1
1 2
1 2
1 2
1 2
0
1
,
1
, 0
;
, 1
,
, 1
,
+
+
+
+
+
+
+
+
+
+
−
+
+
−
−
θ − θ
θ − θ
θ − θ
=
− −
+
τ
< < ≤ <
θ = ϕ ≤ ≤ θ = ψ ≤ ≤
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
i
i
i
i
i
i
i
i
i
i
θ
θ
i
i
I
D
K D
K
h
h
h
i I
θ N
i I
θ N
где
n
i
n
,
1 2
n
i
D
+
,
1 2
n
i
K
−
— значения функций
( )
,
z t
θ
,
( )
(
)
,
D z t
θ
,
( )
(
)
,
K z t
θ
в точках
(
)
,
n
i
z t
,
(
)
(
)
1 2 ,
i
h n
+ τ
,
(
)
(
)
1 2 ,
i
h n
− τ
;
i
ϕ
,
n
ψ
—
значения функций
( )
z
ϕ
и
( )
t
ψ
в точках
i
z
и
n
t
соответственно.
Конечно-разностная аппроксимация левого краевого условия
приводит к следующему выражению:
1
1
1
1
1
1
1
0
0
1
0
1 2
1 2
2
, 0
,
n
n
n
n
n
n
n
n
D
K R E
n N
h
h
+
+
+
+
+
+
+
n − n
n − n
=
− + −
≤ <
τ
где
1
n
R
+
,
1
n
E
+
— значения функций
( )
R t
и
( )
E t
в точках
(
)
1
1
n
t
n
+
= τ +
.
В результате проведения такой конечно-разностной аппроксимации
приходим к следующему дискретному аналогу прямой задачи (1):
(
)
(
)
(
)
1
0
1 2 0
1 2 1
0
1 2
min 0 max
1 2 1
1 2
1 2
1 2 1
2
2
2
1
1 2
1 2
1 2
2
1
2
0;
,
1
;
1
1 1
1
1
0,
1
, 1
;
0,
1
n
n n
n n
n
n
n n
n
n
n n
n
n
n
n n
i
i
i
i
i
i
i
i
n
n
n
i
i
i
n
n n
I
I
D
D
K R E
h
h
h
n N
D
D D
D
h
h
h
K K
i I
n N
h
−
− −
+
−
+ +
−
−
+
Φ = − +
n + n + n + − + − =
τ
τ
n ≤ n ≤ n
≤ ≤
Φ =
n − +
+
n +
n +
τ
n+ +
−
=
≤ < ≤ ≤
τ
Φ = ψ − n =
≤
0
;
,
0
,
i
i
n N
i I
≤
n = ϕ
≤ ≤
(3)
где
( )
;
n
n
t
ψ = ψ
( )
i
i
z
ϕ = ϕ
. При этом коэффициент диффузии
D
и
гидравлическую проводимость
K
в формулах (3) в промежуточных
точках будем вычислять по следующим формулам:
















