
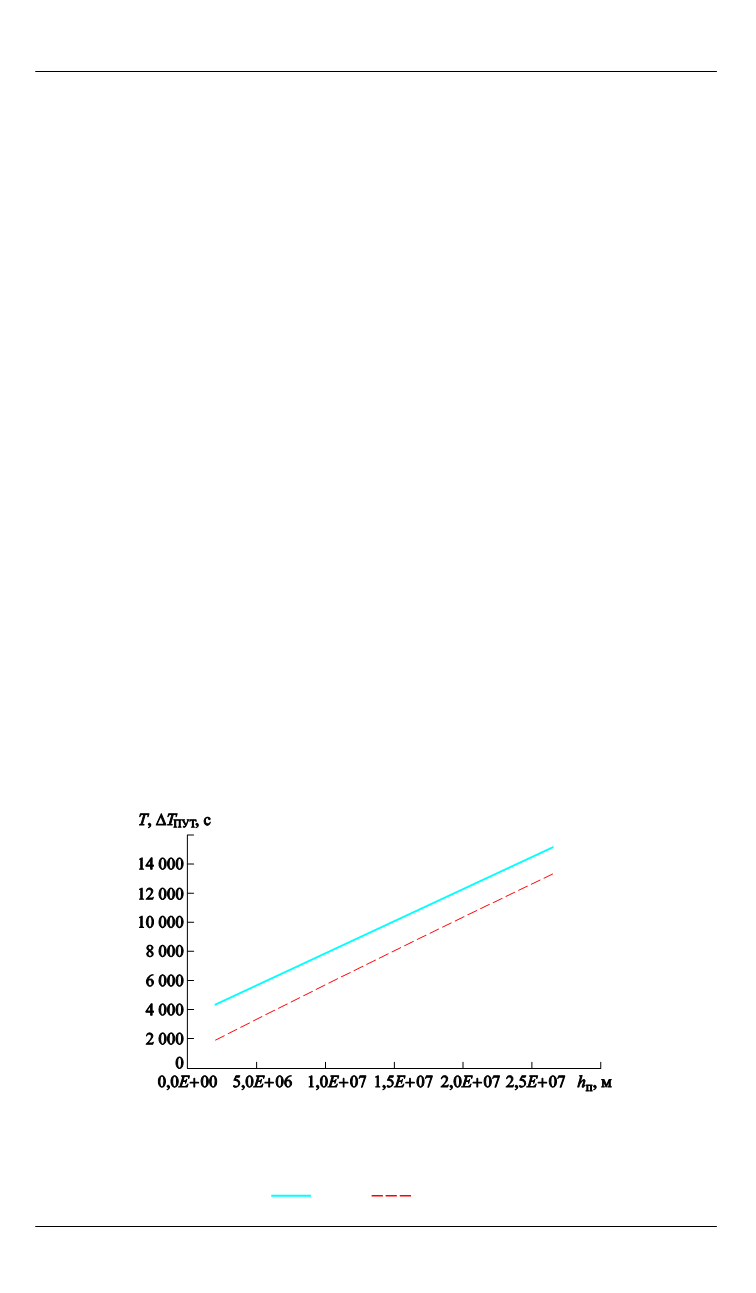
Е.В. Кирилюк, М.Н. Степанов
10
Инженерный журнал: наука и инновации
# 3
⋅
2016
π
( ) [2000; 26371]
=
h T
км,
( ) 26371
=
a
h T
км,
Ω( ) 0
=
T
,
ω( ) 270
=
T
,
( ) 63, 43
=
i T
.
Иными словами, рассматриваем семейство оптимальных переходов
для диапазона значений эксцентриситета целевой орбиты
( ) [0; 0,593]
=
e T
при неизменных круговой НОО и точке начала
решения на ней — в данном случае точки
A
2
.
Результаты приведены для значения коэффициента компромисса
7
10
=
k
. Численные исследования показали, что данное значение
достаточно велико, чтобы задачу минимизации функционала (5)
рассматривали в предельном случае, соответствующем максими-
зации массы выводимого ПГ без ограничения на полное время
выведения. Дальнейшее увеличение коэффициента компромисса
приводит к пренебрежимо малому увеличению конечной массы ОБ
(примерно
5
6
10 ...10
−
−
% от начальной массы ОБ).
Изменение полного полетного времени
T
и продолжительности
пассивного участка траектории (ПУТ)
ПУТ
Δ
T
в зависимости от
значения
h
п
целевой орбиты проиллюстрировано соответствующими
графиками (рис. 3). Аналогичные зависимости для моментов первого
включения ДУ на активном участке траектории (АУТ)
АУТ1
T
и
времени начала ПУТ
ПУТ
T
приведены на рис. 4; для длительностей
включений
АУТ1
Δ
T
,
АУТ2
Δ
T
— на рис. 5.
Графики изменения аргументов широты соответствующих точек
включения и выключения ДУ в зависимости от высоты перигея
представлены на рис. 6, 7.
Рис. 3.
Зависимости полной продолжительности выведения
и длительности ПУТ от значения высоты перигея целевой
орбиты при фиксированной высоте апогея:
—
Т
;
— ∆
Т
ПУТ


















