
В.О. Гладышев, А.А. Терешин, А.В. Яворский, Д.Д. Базлева
10
ную через точку 0, и суммарным значением угла преломления
13
на
выходе луча из линзы и угла
6
,
определяющего нормаль, проведен-
ную через точку 6 соответственно при отсутствии и наличии движе-
ния линзы.
Рассчитав
0
,
,
d d
вычислим, насколько отклонится луч при его
попадании на поверхность Земли с учетом движения линзы по орбите:
0
0
tg
;
dl
d h
tg
,
dl
d h
где
0
dl
— расстояние, на которое отклонится луч от источника излу-
чения при попадании его на поверхность Земли при отсутствии дви-
жения линзы по орбите;
dl
— расстояние, на которое отклонится луч
от источника излучения при попадании его на поверхность Земли,
если линза движется по орбите со скоростью около 7 500 м/с.
Расчеты проведены для двух случаев: луч падает на линзу справа
и слева. Следует отметить, что движение линзы при этом осуществ-
ляется влево для демонстрации симметричности рассчитываемых
значений.
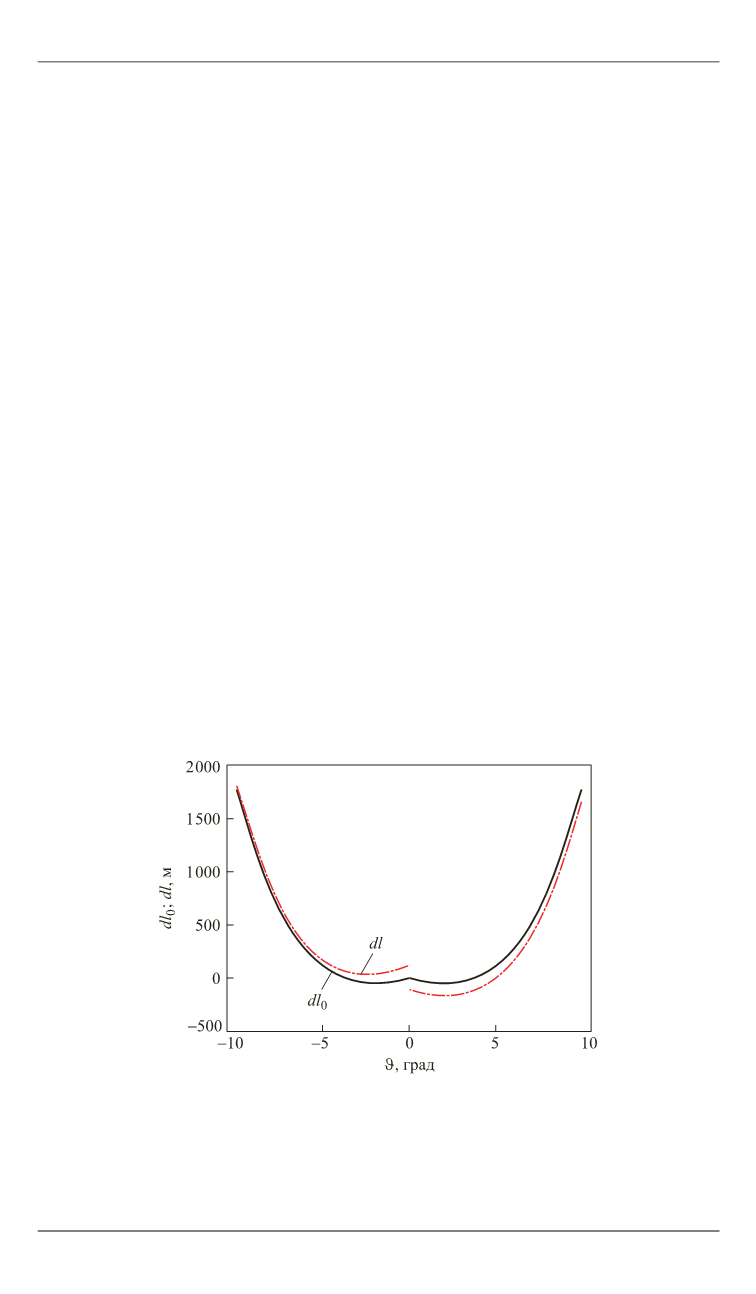
Полученные результаты.
На основании данных расчета построе-
ны графики зависимостей
0
0
,
,
,
( )
dl
dl
d
d
(рис. 3 и 4).
Как видно из графика, представленного на рис. 3, существует ин-
тервал значений, принимаемых углом падения
, в котором разность
Рис. 3.
Зависимости
0
dl и dl
от угла
падения луча при
отсутствии и наличии движения линзы по орбите (левая
часть графика — луч падает справа,
v
= –7 500 м/c; пра-
вая часть графика — луч падает слева,
v
= 7 500 м/c)

















