
Моделирование операции приближения космического манипуляционного робота…
9
Рис. 6.
Внешний вид рассчитанного
эллипса (сплошной контур)
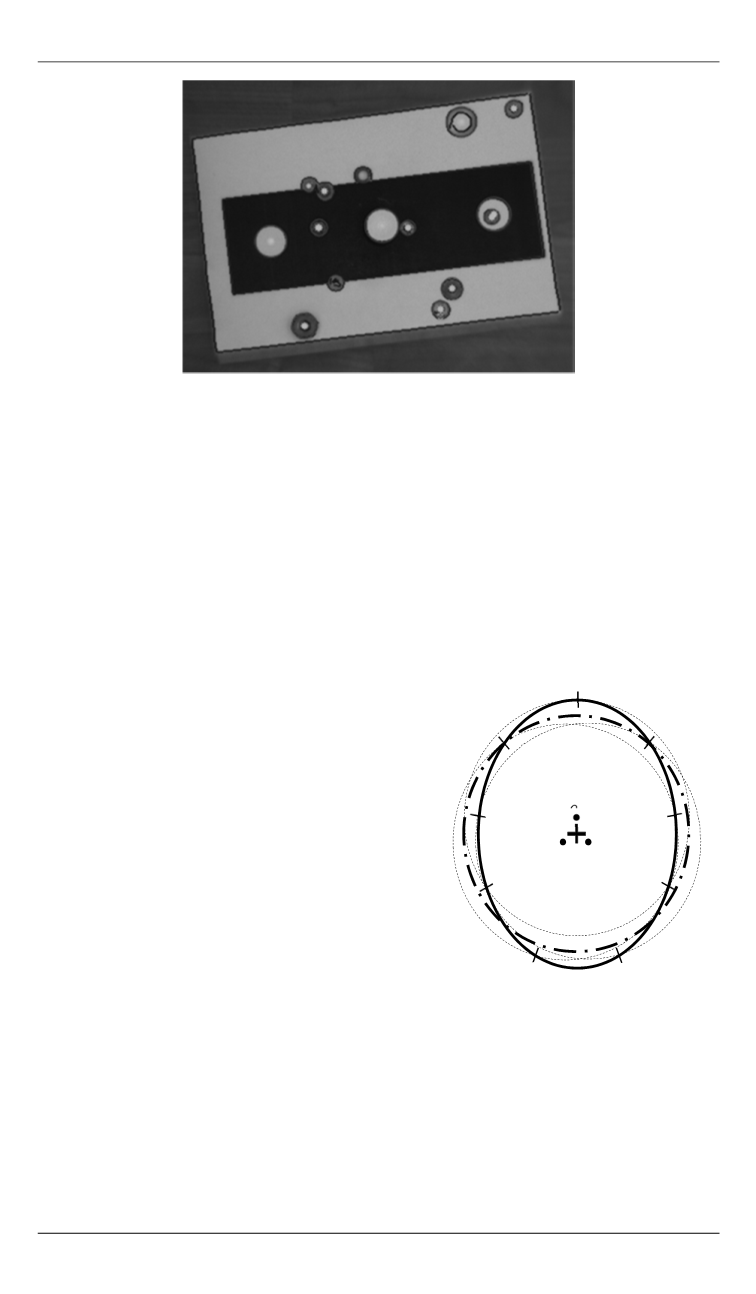
Рис. 5.
Выявленные в кадре окружности
Так же, как и при поиске окружностей, в каждом из контуров с
K
точками выбирается некоторое число
C
троек точек, равномерно рас-
пределенных по длине контура и равноотстоящих одна от другой на
расстояние
K/
3. Для каждой тройки вычисляются координаты и ра-
диус окружности. Если оказалось, что по всем взятым на контуре
тройкам можно построить окружности и расхождение координат
центров этих окружностей не превышает некоторого заданного зна-
чения
A
, то контур считается окруж-
ностью.
Если максимальное расстояние
между центрами проведенных окруж-
ностей больше
A
, но не превышает
предельного для эллипса значения
e
A
,
контур считается эллипсом (рис. 6).
Центр эллипса (см. рис. 6, обозначен
крестом) определим как точку, равно-
удаленную от центров всех окружно-
стей. На рисунке для простоты пока-
заны только три окружности с центра-
ми
1
,
O
2
,
O
3
O
(см. рис. 6, штрих-
пунктирная линия). Окружность, цен-
тром которой является точка, обозна-
ченная крестом, имеет радиус
R
. При
необходимости можно рассчитать параметры эллипса, используя рас-
стояние
l
от центра эллипса до любого из центров окружностей.
Большой радиус эллипса будет на
l
больше среднего значения
ср
R
радиусов построенных окружностей, а малый радиус на
l
меньше.
Т
11
Т
12
Т
13
Т
21
Т
22
Т
23
Т
31
Т
32
Т
33
О
1
О
3
О
2

















