А.А. Панкратов
6
2
2
2
2
0
т
т
1
1 1
1 1
det
0;
I
l
F
F
E
a a
(22)
2
2
2
2
2
2
т
т
т
1
2
2
1 1
2 1
2 1
2
2
2
2
2
2
т
т
т
1
2
2
1 2
2 2
2 2
2
2
2
2
2
2
т
т
т
1
2
2
1 2
2 2
2 2
det
I
I
I
J
J
J
N l
N l
F
F
F
a
a
F
F
F
E
a
a
F
F
F
E
a
a
a
a a
0.
(23)
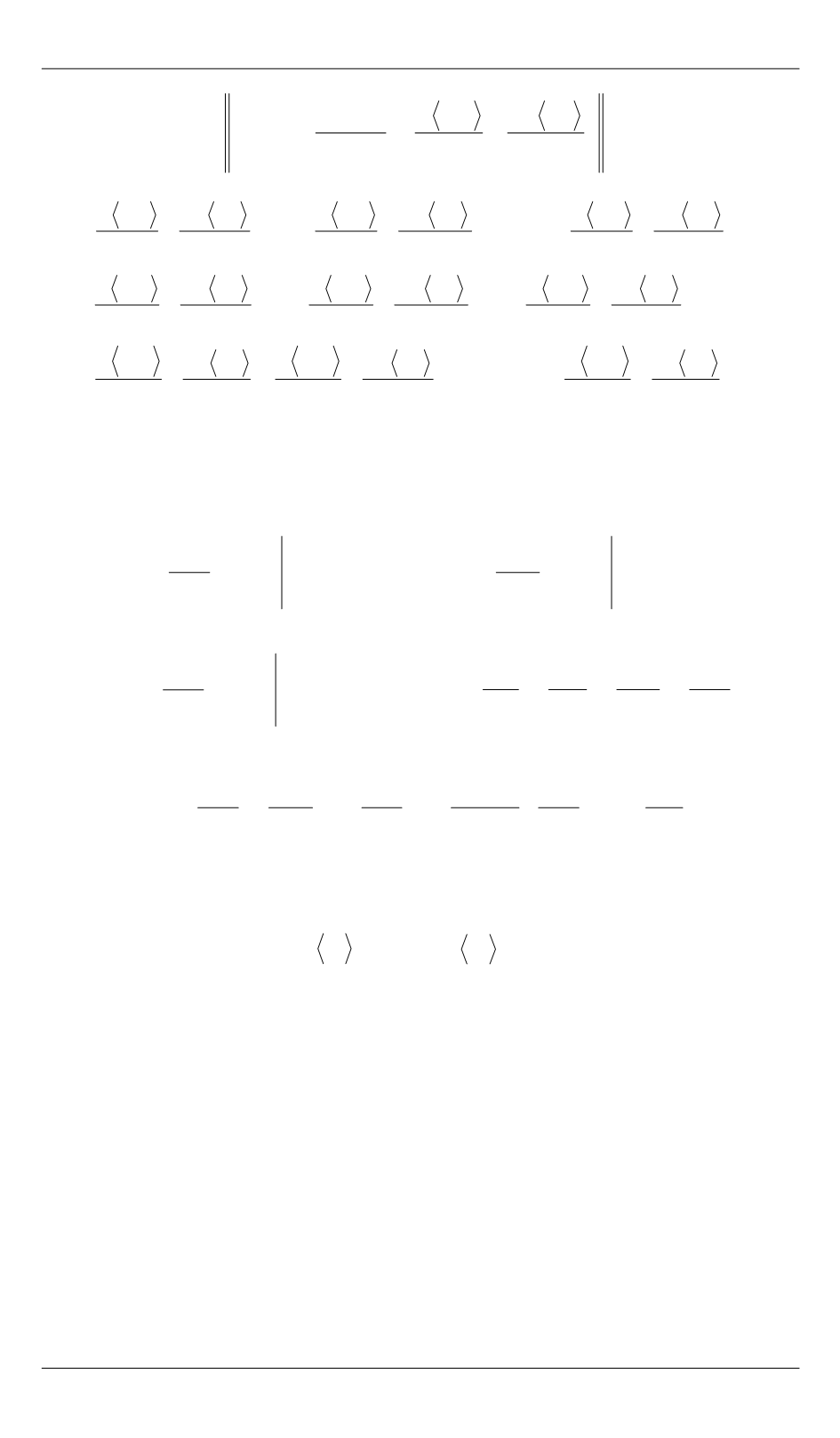
Для краткости записи введем следующие обозначения:
0 1
0 2
0 1
0 2
т
,
,
0
,
;
I
I a J a
V Wdt
0 1
0 2
0 1
0 2
т
,
,
0
,
;
J
I a J a
V Wdt
0 1
0 2
0 1
0 2
т
,
,
0
,
;
I a J a
V Wdt
J
1
1
1
1
0
0
0
0
,
,
,
;
F F F F
V
I
J
2
1
1
1
0
1
1
т
т
т
т
т
т
0
0
0
0 0
0
0
,
,
,
.
F F F
F F
F
W
dt
J
I I
I
(24)
Для периодических функций
(0)
0 0
0 0
, ,
, ,
f
f I J n t
t
исполь-
зуем представление
,
f
f
f
где
f
— постоянная составляю-
щая периодической функции
f
(см. (14)), а
f
— ее чисто периоди-
ческая часть,
0
0.
T
f dt
Для выражения (16) сформулируем достаточное условие суще-
ствования периодических решений и соответствующие результаты по
устойчивости этих решений в виде теоремы.
Теорема 3.
Пусть порождающее семейство периодических решений
таково, что для усредненной по периоду вдоль этого семейства функции
1
F
выполняется условие (16). Тогда система (1)–(3) будет допускать
изолированное, голоморфное по
,
периодическое, с периодом
Т
реше-
ние, обращающее при
0
в порождающее решение (4), если парамет-


