
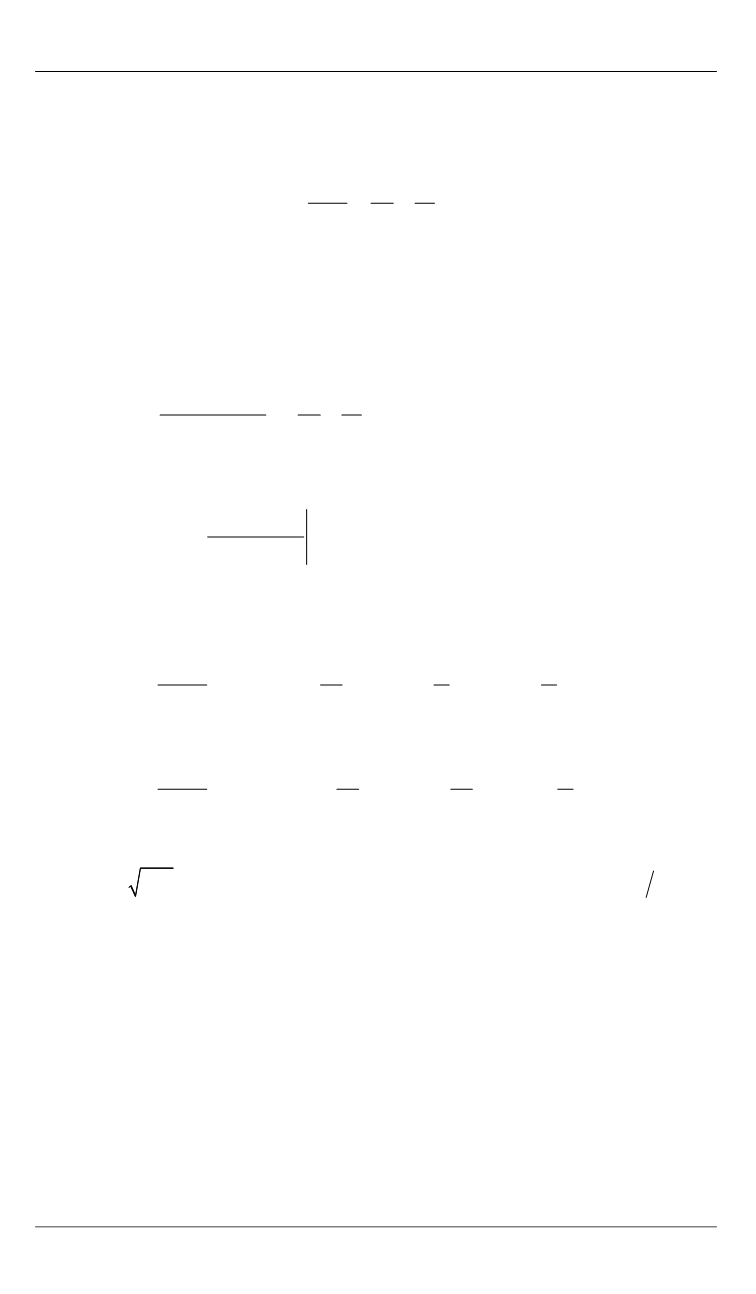
Распределение неосновных носителей заряда…
3
В этом случае время жизни ННЗ описывается соотношением, указан-
ным в [10], которое в рамках модели независимых источников можно
записать в виде
0 1
1 1
( )
( )
b z
z
,
где
0
— время жизни ННЗ в области без дефекта;
1
— время жизни
ННЗ внутри дефекта;
b
— физический размер дефекта;
( )
z
— дель-
та-функция.
Тогда дифференциальное уравнение принимает вид
2
0
0
0
2
0 1
( , )
1
( )
( , )
( ) (
)
d p z z
b
D
z p z z
z z z
dz
с граничными условиями
0
0
0
( , )
(0, )
s
z
d p z z
D
v p z
dz
,
0
( , ) 0
p z
.
В работе [13] получено решение этого уравнения:
0
0
1
0
1
0
0
0
0 1
0
1
( ) exp
exp
exp
0,
;
2
,
( ) exp
exp
exp
, .
2
L
z
z
z
z
S
z
z
DS
L
L
L
p z z
L
z
z
z
z S
z z
DS
L
L
L
Здесь
0
L D
— диффузионная длина ННЗ;
1
1
/
/
/
s
S D L v b D L
1
/
s
v b
— коэффициент.
Для расчетов распределений ННЗ в случаях однородного полу-
проводника и полупроводника с дефектами на поверхности были взя-
ты следующие значения электрофизических параметров:
1 мкм
L
,
8
0
10 с
,
11
1
10 c
,
8
2
10 мкм /с
D
,
7
10 мкм/с
s
v
, энергия пер-
вичных электронов пучка
0
20 кэВ
E
, мощность пучка первичных
электронов
0
10 Вт
P
, размер дефекта принимали равным
2
10 мкм
.
Значения
0
( )
z
рассчитывали с помощью полученных для диффузи-
онной модели формул, указанных в [1]:

















