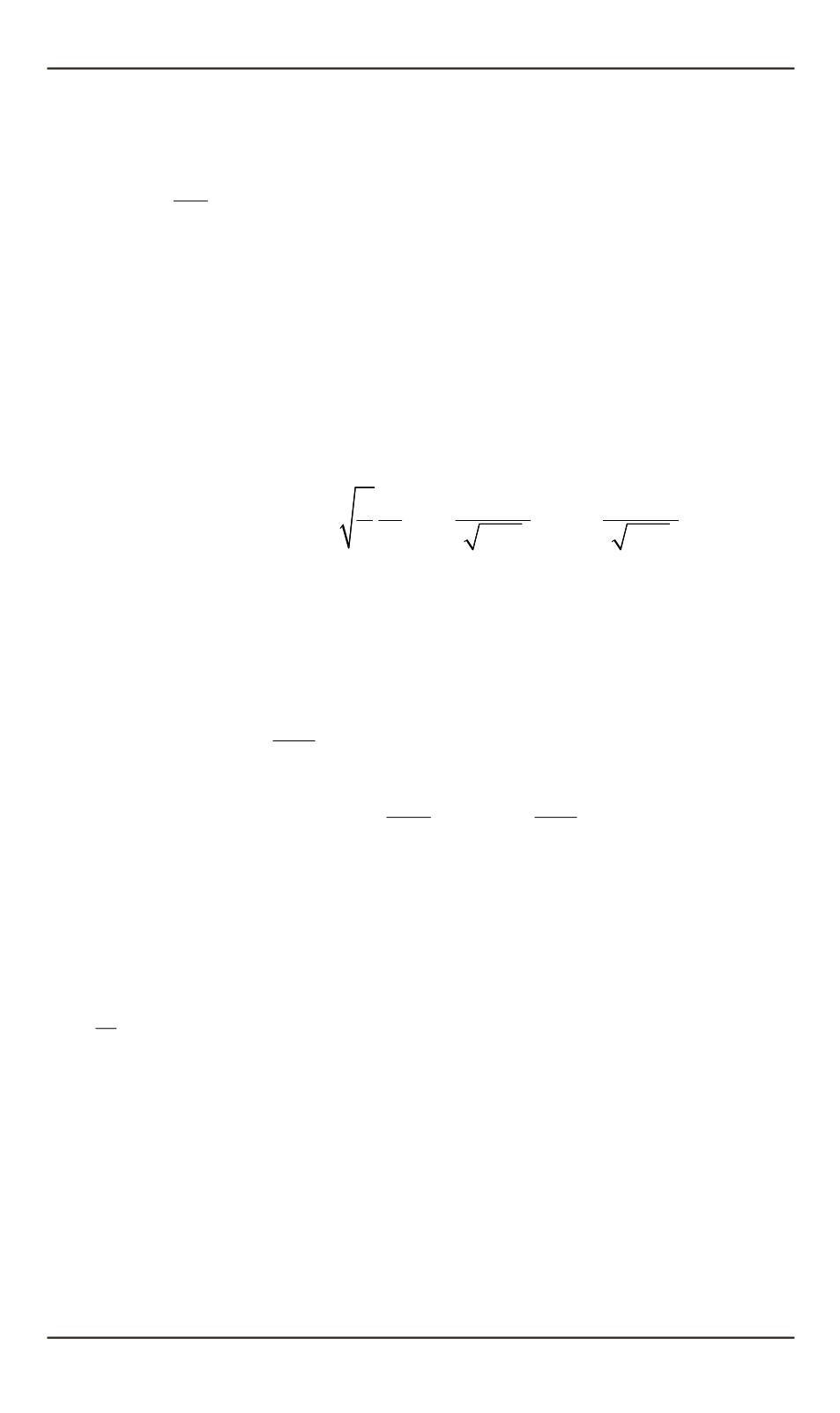
7
Движение твердого тела в вязкой жидкости при больших числах Рейнольдса
Составим уравнения изменения кинетического момента для систе-
мы тело – жидкость в области
D
R
:
( )
(
)
0
0
,
.
r
r
r
S
S
D
dK r p ndS r Tn
n dS M
dt
K m r u J
r dD
′
= − × + × − ρυ υ +
⎡
⎤
⎣
⎦
= × + θ + ρ × υ
∫∫
∫∫
∫
Здесь
J
0
– тензор инерции твердого тела относительно полюса
O
1
.
Проводя выкладки, аналогичные предыдущим, и опуская громозд-
кие вычисления, запишем уравнения изменения кинетического момен-
та системы тело – жидкость в виде
(
)
(
)
( )
( )
(
)
0
0
0
*
*
0
0
0
,
t
t
t
t
G
d
u d
v d
J J m r u u
C
D
dt
t
t
M G r r g
⎡
⎤
θ τ τ
τ τ
+ θ + × + Γ +
+
=
⎢
⎥
π
− τ
− τ
⎢
⎥
⎣
⎦
= + ρ − ρ ×
∫
∫
(27)
где
J
,
Γ
*
,
C
,
D
*
– тензоры с компонентами
*
*
,
,
,
ij
ij
ij
ij
J
C D
Γ
(
i, j
= 1, 2, 3),
определяемые следующими формулами:
(
)
(
)
(
)
(
)
(
)
*
*
;
;
;
;
i
ij
i
i
i
S
S
j
i
ij
i j
i
j
ji
S
S
S
ij
j
j
i
i
ij
S
ij
j
i
i
i
S
J
dS
r n e dS
n
n dS
dS
dS
n
n
D
e r e
dS D
C r e
r e
dS
∂Ψ
= Ψ = Ψ ×
∂
∂Φ
∂Ψ
Γ = Ψ = Ψ = Φ = Γ
∂
∂
= ∇Φ − × + ∇Ψ =
= × + ∇Ψ × + ∇Ψ
∫
∫
∫
∫
∫
∫
∫
G G
(28)
1
G
G
r
rdG
G
=
∫
– центр давлений.
Уравнения (26) и (27) полностью описывают динамику тела
в жидкости. К ним необходимо добавить начальные условия в виде
( ) ( ) ( ) ( )
0
0
0
0
,
,
,
.
u t
t u t
t
θ
θ
При
ν
=
0 уравнения переходят в известные
уравнения тела в идеальной жидкости.
Влияние вязкой жидкости на движение тела определяется тензор-
ными коэффициентами
E
,
D
,
C
. Эти коэффициенты выражаются толь-
ко через потенциалы Стокса – Кирхгофа, т. е. через решения задачи
о движении тела в идеальной жидкости.