Простой алгоритм терминального управления пневмоприводом…
9
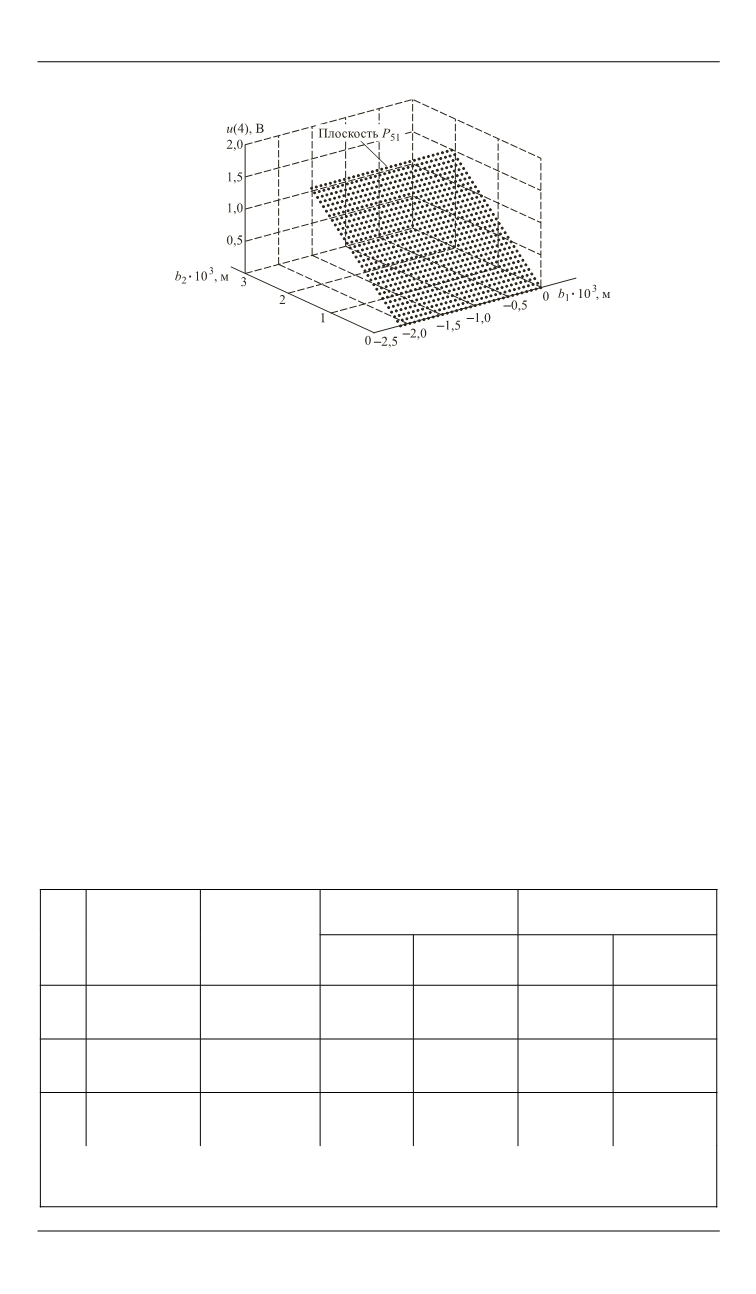
Рис. 7
. Плоскость переключения для пятого интервала управления
Алгоритм работы
:
51
4
u
P
.
Моделирование показало, что предложенный ПП-алгоритм, имея
очень высокое быстродействие, позволяет получить хорошую терми-
нальную точность во всем диапазоне перемещения штока пневмо-
привода. В таблице представлены некоторые результаты терминаль-
ных значений желаемого
*
2
T b
и полученного
T
выходного
угла при различных значениях
1 2
,
.
b b
Видно, что точность перевода
системы в конечную точку весьма высока.
В качестве примера приведем также графики моделирования рас-
смотренной выше задачи быстродействия с использованием ПП-
алгоритма. На рис. 8 представлены графики изменения угла
t
, пе-
ремещения штока
t
и управления
u t
. Перевод осуществляется
практически за то же время, при этом отсутствует выход на ограничи-
тель или скользящий режим и затраты энергии значительно меньше.
Результаты тестирования СМ- и ПП-алгоритмов
*
3
max
(
0, 0021 м,
7, 4 10 c)
b
T
№
п/п
Начальное
положение
штока
1
0 ,
b
м
Конечное
положение
штока
*
2
,
b
T
м
Моделирование
СМ-алгоритма
Моделирование
ПП-алгоритма
,
T
м
,
T
м/с
,
T
м
,
T
м/с
1
*
0,1
b
=
= – 0,0002
*
0,95
b
=
= 0,001995
0,0020
–0,0012
0,0020
–0,0014
2
*
0,9
b
=
= – 0,00189
*
0,5
b
=
= 0,00105
0,0010
–0,0027
0,0010
–0,0026
3
*
0,9
b
=
= – 0,00189
*
0,1
b
=
= – 0,0002
0,199
10
–3
–0,463
10
–3
0,198
10
–3
–0,764
10
–3
П р и м е ч а н и е. При переходе от углов
1
2
0,
0
b b
к
1
2
0,
0
b b
кусочно-
постоянное управление меняет свой знак на противоположный.


