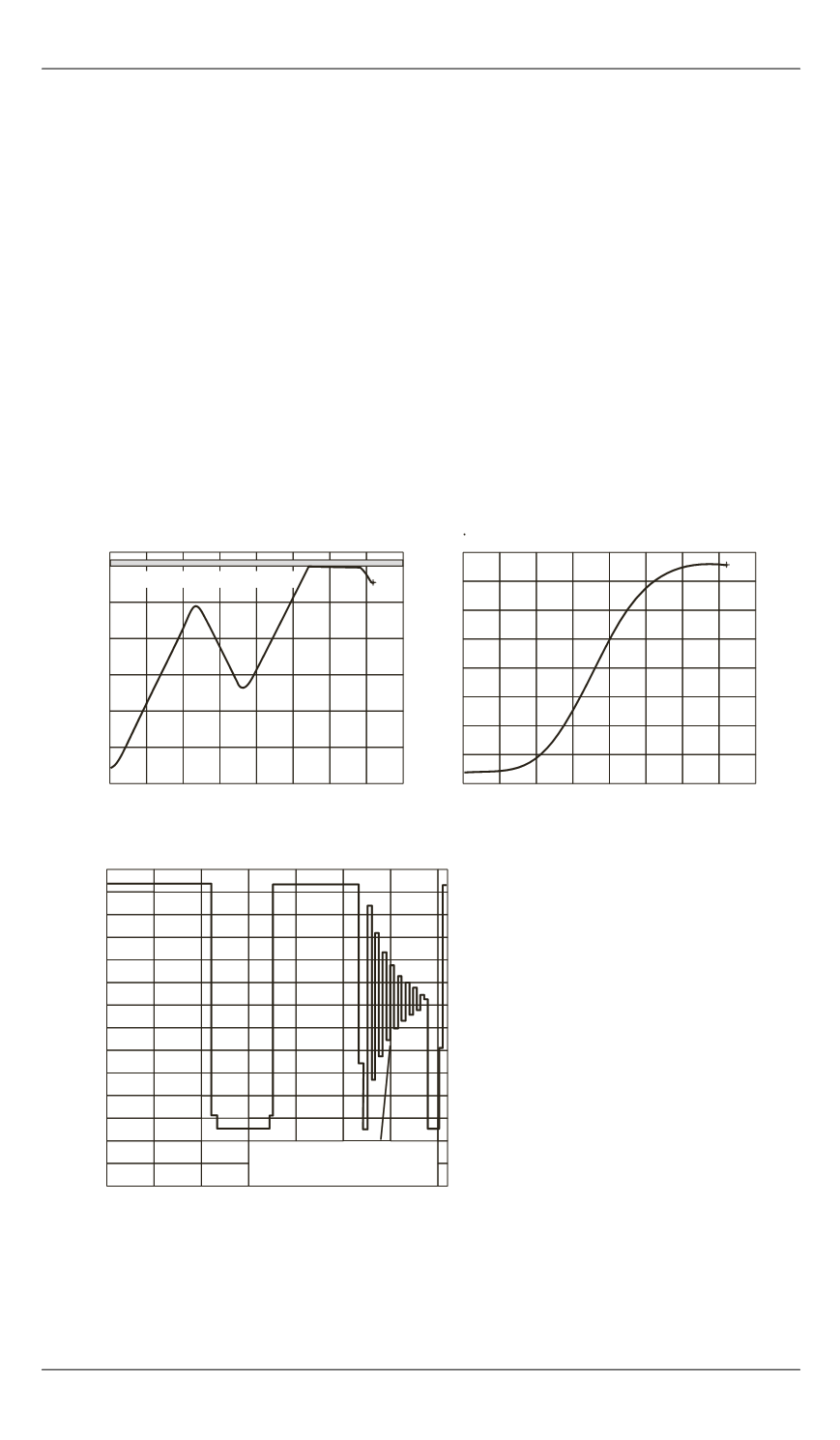
Простой алгоритм терминального управления пневмоприводом…
5
3
1
0
1,8 10
b
м в конечное
3
2
1,8 10
T b
м. Движение по
границе осуществляется в скользящем (при выбранном шаге дискрети-
зации
/
h T N
) режиме.
На рис. 2 представлены графики оптимального по быстро-
действию перевода системы из состояния
3
1
0
1,8 10
b
м
в состояние
*
3
2
1,8 10
T b
м с использованием СМ-алгоритма.
Числовые характеристики моделирования: число шагов дискре-
тизации
80
N
, число итераций
iter
174,
N
3
1,801 10
T
м,
0, 0007
T
м/с. Полученные траектории системы и управление
(см. рис. 2) практически совпадают с результатами работы [1] за ис-
ключением прохождения границы: в статье [1] — выход на упор и
прижим к ограничителю, в данной работе — скользящий режим.
Рис. 2.
Графики оптимального по быстродействию перевода системы из
состояния
3
1
0
1,8 10
b
м в состояние
*
3
2
1,8 10
T b
м с ис-
пользованием СМ-алгоритма:
а
— изменение угла
;
t
б
— перемещение штока
;
t
в
— график управления
u t
0,015
0,010
0,005
0
0,005
0,010
0,015
0 1 2 3 4 5 6
, рад
1
0
1
2
0 1 2 3 4 5
2
а
б
0 1 2 3 4 5 6
u t
( ), В
20
10
0
10
20
Движение по границе
в скользящем режиме
в
0
Ограничение по углу
t
10
3
, c
6
10
3
, м
t
с
t
с


