Симплекс-метод решения задачи быстродействия при наличии ограничения…
9
Заключение.
Моделирование задачи линейного программирования
с помощью симплекс-метода показало, что если не стремится к чрез-
мерной
по времени
точности перевода в терминальную точку, то 30…60
точек дискретизации вполне достаточно. Предложенный алгоритм
можно с успехом применять для решения практических задач.
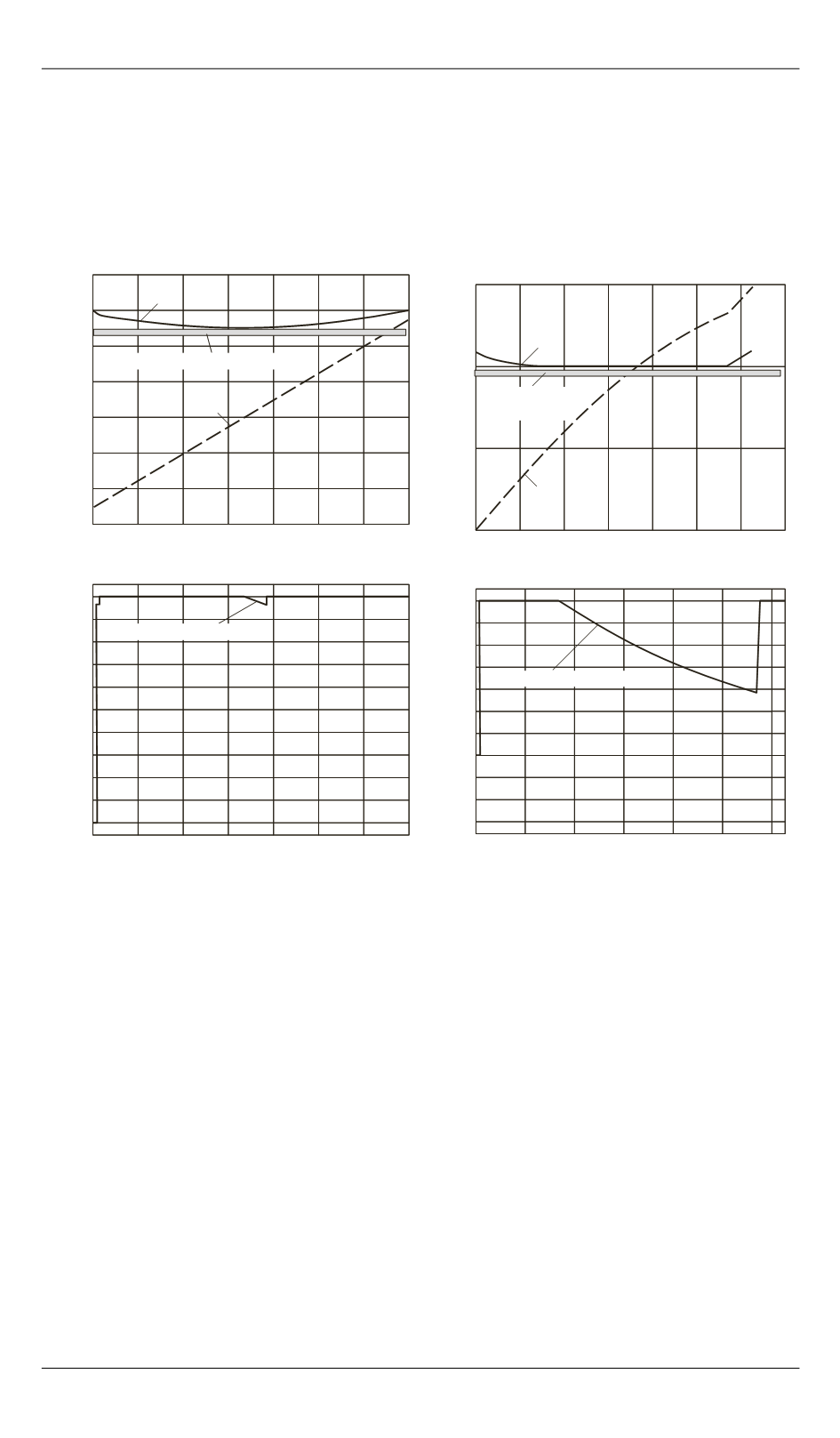
Рис. 1.
Графики координат состояния (
а
)
и управления (
б
) для промежуточного
времени
1
7 0,7
t
с (время меньше
минимально необходимого)
Рис. 2.
Графики координат состояния
(
а
) и управления (
б
) для оптимального
времени
*
1
1,25
t
с
ЛИТЕРАТУРА
[1] Гамкрелидзе Р.В. Оптимальные процессы управления при ограниченных
фазовых координатах.
Известия АН СССР. Сер. Математика
, 1960, № 3,
с. 315–356.
[2] Дубовицкий А.Я., Милютин А.А. Необходимые условия слабого экстре-
мума в задачах оптимального управления со смешанными ограничениями
типа неравенства.
Журн. вычисл. математики и мат. физики
, 1968, т. 8,
№ 4, с. 725–779.
[3] Пупков К.А., Фалдин Н.В., Егупов Н.Д.
Методы синтеза оптимальных си-
стем автоматического управления
. Москва, Изд-во МГТУ им. Н.Э. Баумана,
2000, 512 с.
0 0,1 0,2 0,3 0,4 0,5 0,6
t
, c
1,0
0,8
0,6
0,4
0,2
0
0,2
0,4
0,6
0,8
1,0
u
( )
t
Движение по границе
а
б
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
0 0,1 0,2 0,3 0,4 0,5 0,6
t
, c
x t
1
( )
x t x t
1 2
( ) ( )
;
x t
2
( )
Ограничение на координату
x
1
0,2 0,4 0,6 0,8 1,0 1,2
t
, c
0,5
1,0
1,5
0
0
x t
1
( )
X t x t
1 2
( ) ( )
;
x t
2
( )
Ограничение
координаты
x
1
0 0,2 0,4 0,6 0,8 1,0
t
, c
1,0
0,8
0,6
0,4
0,2
0
0,2
0,4
0,6
0,8
1,0
u
( )
t
Движение по границе
а
б


