Моделирование устойчивости сжатого и скрученного стрежня
7
2
3
2
2
2
1
sin 2 cos 2 cos 2 sin 2
4
sin 2 sin 2
cos 2 1 cos 2
cos 2 1 cos 2
1 sin 2 sin 2
cos 2 1 cos 2
1 cos 2 1 cos 2
0.
c
c
c
c
c c
c c c
c
c
c
c c
c c c
c
c
c
(11)
Из уравнения (10) находим угол
кр
при чистом осевом сжатии
стержня, когда
0,
M
0,
.
c B A
Решая уравнение (11), опре-
деляем угол
кр
при
0,
P
0
M
или
0,
P
0.
M
Нетрудно по-
казать, что при чистом кручении
( 0,
c
)
B A
уравнение (11)
совпадает с уравнением (3). Изменение угла
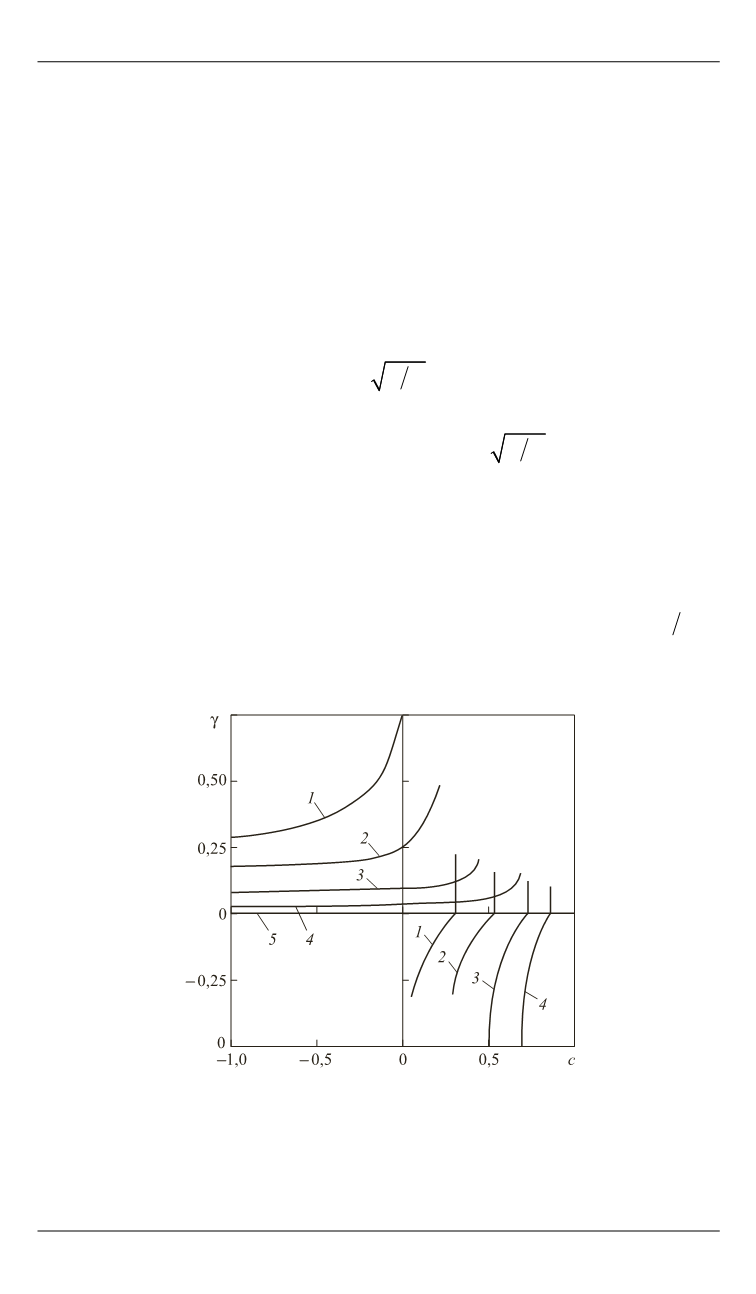
в этом случае приве-
дено на рис. 3: кривые претерпевают разрыв непрерывности, обу-
словленный тем, что с увеличением крутящего момента от нуля до
некоторого значения критическая сила
кр
P
возрастает, затем начина-
ет убывать и переходит через эйлеровское значение, которому соот-
ветствует разрыв непрерывности. С приближением отношения
В А
к
единице кривые изменения приближаются к оси абсцисс, т. е. усили-
вается влияние кручения на устойчивость стержня.
Рис. 3.
Изменение параметра устойчивости стрежня в виде консоли
при
k
= 0,1 (
1
); 0,3 (
2
); 0,5 (
3
); 0,7 (
4
); 1,0 (
5
)
При
A
=
B
характеристическое уравнение имеет единственный
корень, равный нулю, и, согласно (10), параметр
0
. Таким обра-


