Моделирование устойчивости сжатого и скрученного стрежня
5
где
.
1
B A c
c B A
(9)
При изменении отношения
B A
в пределах
0
1, 0
B A
пара-
метр
также находится в пределах 0
1, 0.
В общем случае, когда
,
A B
0,
P
0,
M
уравнения (6) можно
решить следующим образом. Задавая различные значения
B A
в интер-
вале от 0 до 1,0 и изменяя при каждом из них параметр
с
от –1,0 до
B A
по формуле (9), определяем соответствующее значение
. Затем,
решая уравнение (8) при каждом значении
sin
sin
cos
C C
C
sin
sin
cos
0,
C
находим наименьший, не равный нулю, ко-
рень каждого из них. Из каждой пары полученных корней выбираем
меньший, который и является критическим значением
кр
.
Подста-
новка найденного значения
кр
в формулу (7) при
0,5
позволяет
получить соответствующее значение параметра
.
Изменение пара-
метра
при различных значениях
k B A
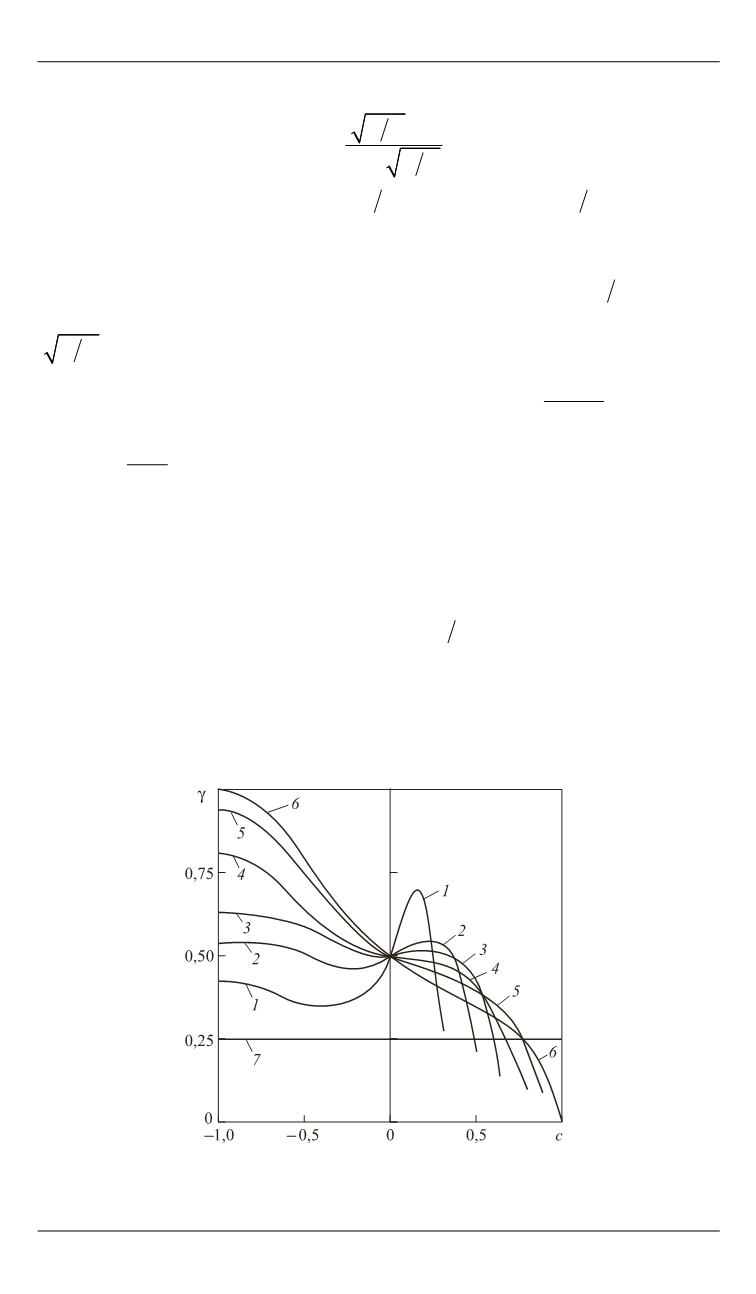
приведено на рис. 1. В
случае стержня с шарнирными опорами как при осевом, так и при сле-
дящем крутящих моментах задача сводится к решению двух незави-
симых уравнений:
sin cos
cos sin 0;
c
c
cos sin sin cos
0.
c
c
Рис. 1.
Изменение параметра устойчивости стрежня с шарнирными опорами
при
k
= 0,1 (
1
); 0,3 (
2
); 0,5 (
3
); 0,7 (
4
); 0,9 (
5
); 1,0 (
6
); 0 (
7
)


