Моделирование упругопластического поведения материала…
9
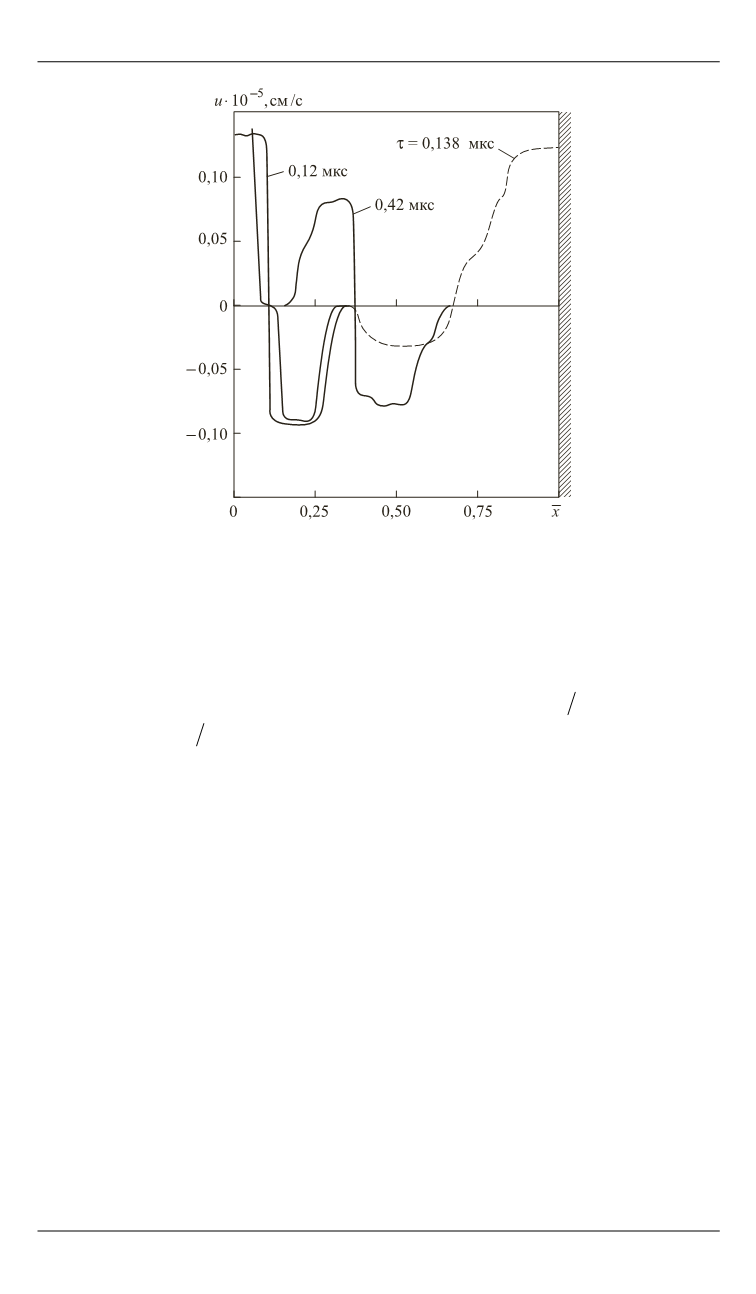
Рис. 3.
Распределение массовой скорости в разные моменты времени
возмущения по половине прогретого слоя
( 0,12 мкс),
волны, иду-
щие с границ прогретого слоя, смыкаются. Распространение волн раз-
грузки и сжатия вызывает движение всего нагретого материала, что ве-
дет к возникновению растягивающих напряжений. Амплитуда распро-
страняющейся внутрь материала волны сжатия
0
1 2 ,
r
массовая
скорость
2.
u u
За ударной волной следует волна разгрузки с ам-
плитудой
0
.
r
За волной разгрузки напряжение скачком убывает до
нуля
( 0, 42 мкс).
На этой кривой наблюдаются участки, соответ-
ствующие упругому предвестнику и упругой волне разгрузки.
Наличие жесткой поверхности у материала второго слоя исклю-
чает движение внутренней границы первого слоя. После отражения
от жесткой поверхности распределение напряжения и скорости
( 0,138 мкм)
представлено на рис. 2, 3 (штриховая кривая). Про-
филь скорости и напряжения искажается из-за наличия диссипатив-
ных механизмов и в результате взаимодействия волн при отражении
от жесткой поверхности. При расчетах вычисляли полную подведен-
ную тепловую, механическую, полную внутреннюю энергию, работу
пластического деформирования. Эти параметры нужны для проверки
дисбаланса энергии. Работа напряжений на пластических деформа-
циях определяется уровнем и характером нагружения, свойствами
конструкционных материалов. Расчеты показывают, что она в основ-
ном возрастает в начальный период, когда интенсивность напряже-
ний превышает предел текучести.


