Т.А. Бутина, В.М. Дубровин
2
2
2
0
2 3
3 1
0
2
1 2
1
6
;
Y
K
(1)
0
0 0
пл
, , ,
,
K K
р W
(2)
где
0
— интенсивность скорости деформаций;
0
— интенсивность
напряжений;
р
— гидростатическое давление;
пл
W
— работа пла-
стического деформирования.
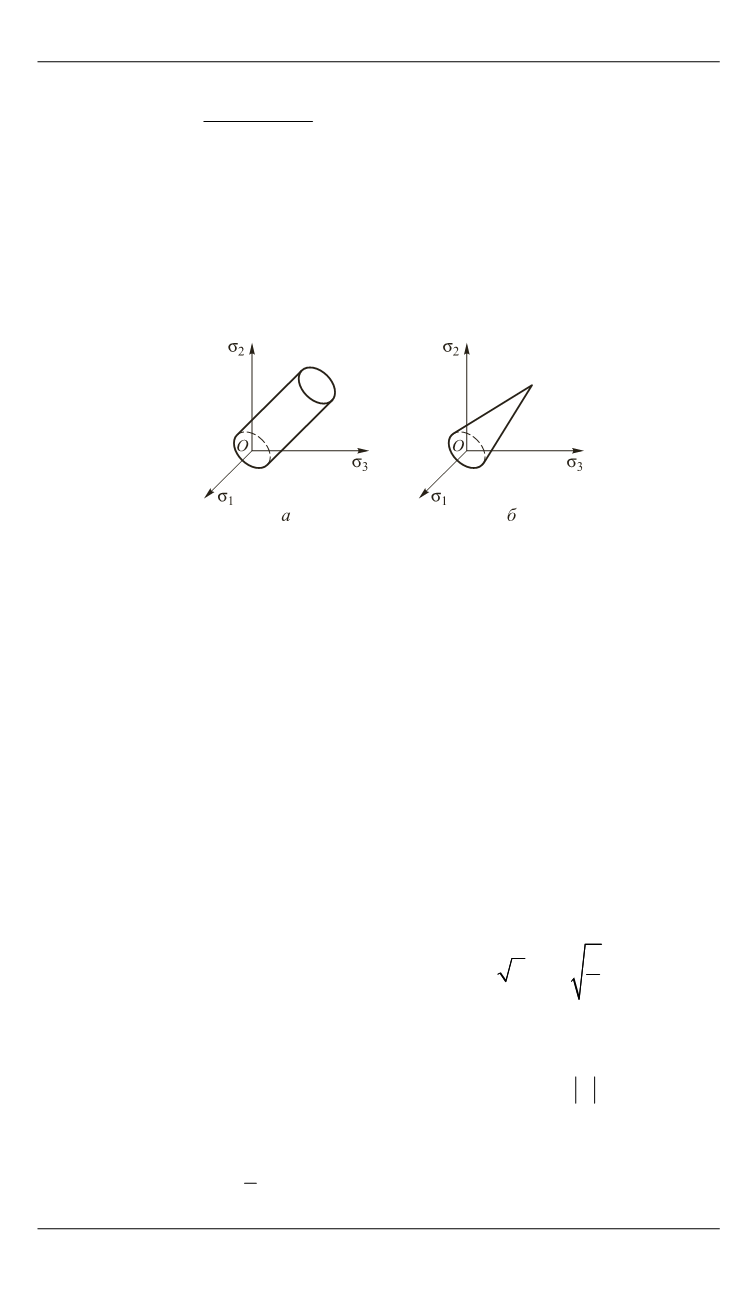
Рис. 1.
Форма поверхности при выполнении условий (3) (
а
) и (4) (
б
)
Функция
K
имеет смысл предела текучести при чистом сдвиге:
1
2 3
1
,
0,
.
K
(3)
В случае использования вместо функции
K
предела текучести
0
Y
(при простом растяжении) условие (1) принимает вид
2
2
2
2
1 2
2 3)
3 1
0
.
(
2
Y
(4)
В общем случае предел текучести
0
Y
является функцией пере-
численных выше параметров:
2
0 0
пл
0 0
, , ,
.
Y Y
P W
Вид функции определяется экспериментально и специфичен для
различных классов материалов. Поверхность текучести (в случае
идеальной пластичности) представляет собой поверхность кругового
цилиндра с радиусом основания, равным
2
K
и
0
2
3
Y
соответ-
ственно.
Обобщенное условие Мизеса имеет вид
2
2
2
1 2
2 3
3 1
6
.
K d р
(5)
Здесь
d
— экспериментальный коэффициент;
p
— гидростатиче-
ское давление,
1 2 3
1
;
3
p
пл
, ,
.
i
i
K
W


