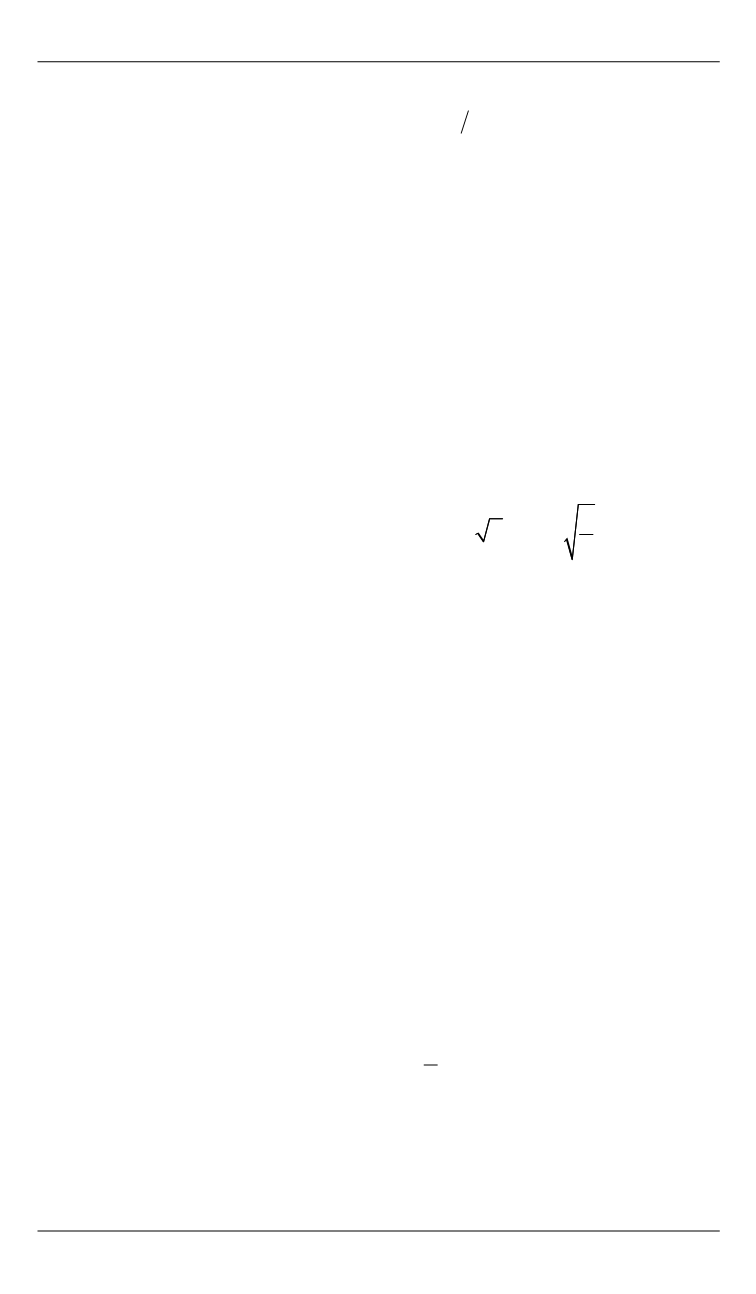
Моделирование упругопластического поведения материала…
3
Поверхность текучести (5) представляет собой поверхность кру-
гового конуса с вершиной
1 2 3
.
K d
Напряженное состояние в произвольной точке, находящейся
внутри конуса или цилиндра, полностью определяется соотношения-
ми теории упругости. Если параметры напряженного состояния соот-
ветствуют точке, лежащей вне этих поверхностей, для расчета возни-
кающего пластического течения корректируют девиатор тензора
напряжений. Ниже показано, что такая корректировка равносильна
использованию для расчета пластичности полных соотношений тео-
рии пластического течения.
Известно, что пластичность материала зависит только от сдвига
при условии, что сумма девиаторов тензора напряжений
1 2 3
0.
S S S
Равнонаклоненная к осям и проходящая через начало координат
плоскость (см. рис. 1,
а
) при пересечении с указанными поверхно-
стями образует круг текучести радиусом
2
K
или
0
2
3
.
Y
Рассмот-
рим в качестве условия пластичности простое растяжение (случай
чистого сдвига может быть получен незначительным пересчетом).
Пластическое течение накладывает ограничение лишь на сдвиговые
напряжения, связанные с пластической деформацией. Причем эта
пластическая часть деформации перпендикулярна кругу текучести.
Если при расчете новое напряженное состояние (точка в простран-
стве
1 2 3
,
,
)
окажется за пределом текучести, скорректированное
напряженное состояние будет находиться на пересечении круга теку-
чести и перпендикуляра, опущенного на него из этой точки. Таким
образом, основная задача корректировки напряженного состояния в
случае наличия пластического течения сводится к сохранению девиа-
тора тензора напряжений на круге текучести [2].
Запишем условие (4) для компонент девиатора тензора напряже-
ний в виде
2
2
2
2
1 2
2 3
3 1
0
2
S S
S S
S S
Y
или с учетом условия
1 2 3
0
S S S
2 2 2
2
1 2 3
0
2
3
.
S S S Y
(6)
При наличии пластического течения полная деформация равна
сумме упругой
y
i
и пластической
пл
i
деформаций:
y
пл
.
i
i
i
(7)