Т.А. Бутина, В.М. Дубровин
8
Как указывалось ранее, предел текучести не зависит от того, про-
исходит сжатие или растяжение материала, которые при этом суще-
ственно различаются (эффект Баушингера). Пусть при сжатии предел
текучести равен
0
,
Y
при растяжении —
0
.
Y
Тогда общее выражение
для определения предела текучести с учетом эффекта Баушингера
имеет вид
'
0 0
0 0
sign
.
2
2
Y Y
V Y Y
Y
V
Рассмотрим двухслойную сферу радиусом 10 см. Допустим, что в
начальный момент часть внешнего слоя, граничащая с вакуумом, про-
грета до температуры
300
С. Температура остальной части этого и
второго слоя равна нулю. Плотность второго слоя в 100 раз больше, чем
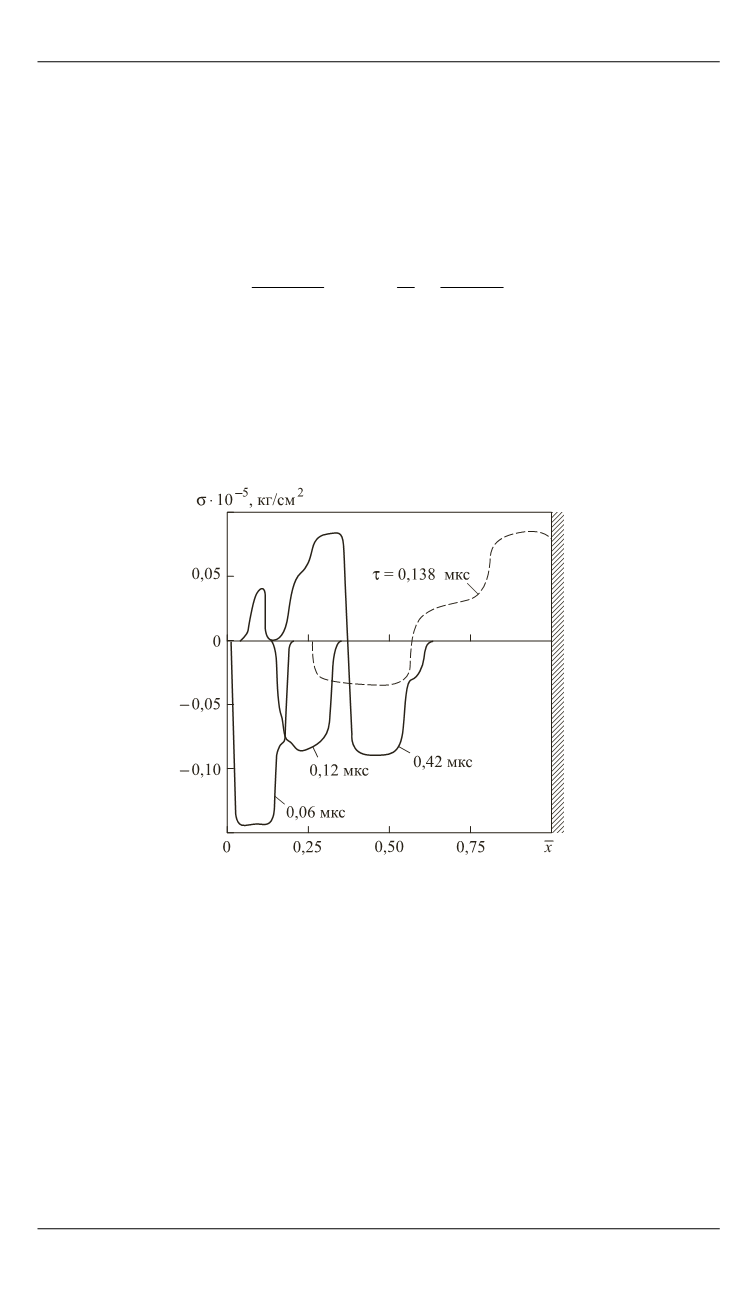
первого. На рис. 2, 3
показано распределение напряжения и массовой
скорости в разные моменты времени, примем за единицу времени
1 мкс. Ясно, что со стороны свободной поверхности и от границы раз-
дела нагретого и холодного вещества распространяются волны разгруз-
ки
( 0,06 мкс),
внутрь материала идет волна сжатия. На наружной
поверхности вследствие полной разгрузки напряжение равно нулю
( 0,12 мкс).
t
Центральная часть нагретого слоя неподвижна, а об-
ласть, граничащая с холодным веществом, движется в сторону, проти-
воположную движению наружной поверхности с вдвое меньшей скоро-
стью. Напряжение в этой области составляет половину первоначального
значения. В момент времени, соответствующий времени пробега
Рис. 2.
Распределение напряжения в разные моменты времени


