Об одной задаче оптимальной остановки марковских цепей
7
цене. Рисунок 5 показывает, что игрок, не склонный к риску, готов
покупать только по самой низкой цене, а стратегию продажи опреде-
ляет верхняя кривая (при продаже этот игрок готов ждать, если есть
надежда достичь нижней границы).
Отметим существенное различие в стратегиях игроков, склонных и
не склонных к риску. Более того, для симметричного случайного блуж-
дания на всей прямой игрок, не склонный к риску, никогда не будет
покупать актив, а склонный к риску игрок купит его сразу же и будет
держать до последнего момента времени. Но при этом средний выиг-
рыш у обоих игроков в любом случае будет одинаковым (нулевым).
3. Модель Эренфестов.
Матрица переходных вероятностей имеет
вид
( , ) 0,
l
i j
Ρ =
если
1,
i j
− ≠
( ,
1) (
)/( 1),
l
i i
n i n
Ρ + = − −
( ,
1)
l
i i
Ρ − =
( 1)/( 1).
i
n
= − −
У этой модели есть разумная рыночная интерпрета-
ция: при стабильной ситуации на рынке цена актива стабилизируется
и при отклонении цены актива от среднего значения спекулятивные
операции с «короткими» деньгами «тянут» ее к среднему значению.
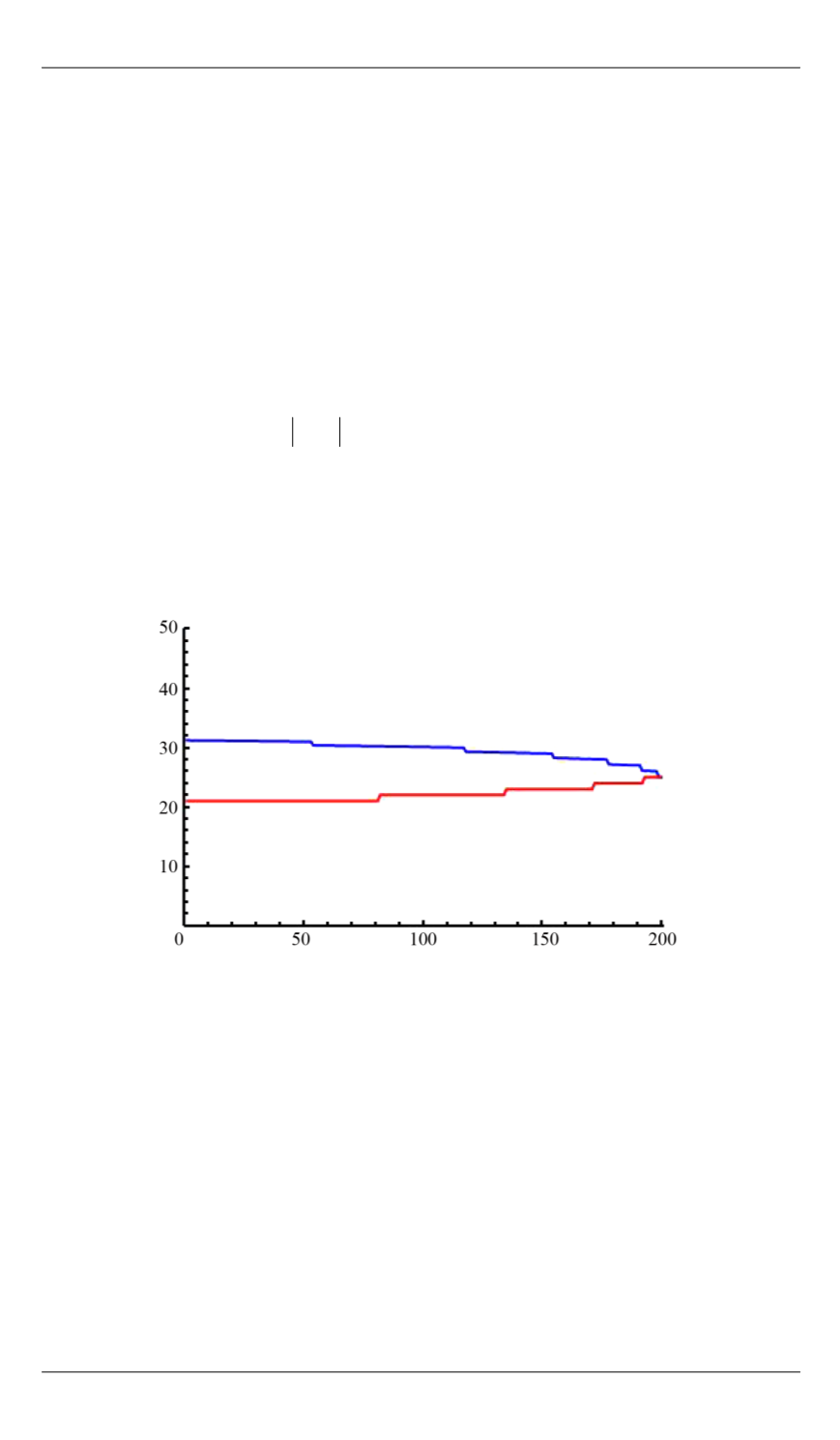
Стратегии для определения
σ
и
τ
представлены на рис. 6.
Рис. 6.
Правила остановки в модели Эренфестов
На рис. 7 дана зависимость средней доходности операции «по-
купка—продажа» от
t
при условии, что
100
,
X t
=
200,
N
=
50.
m
=
График на рис. 8 отражает зависимость средней доходности от
временного интервала, на котором осуществляется процесс игры
(начальное состояние
25
t
=
). Доходность операции «покупка—
продажа» для модели Эренфестов существенно отличается от модели
независимых случайных величин (см. рис. 3). Если для независимых
случайных величин средняя доходность, равная 90 % максимальной,
достигалась на временнóм отрезке [0, 30], то для модели Эренфестов
даже на отрезке [0, 200] она едва достигает 14 % максимально воз-
можной доходности.


