А.В. Анферова, Л.Г. Ветров, А.Л. Сунчалина
4
( )
( )
( )
( )
1
1
1
1
1
1
1
0,
, ;
,
,
, .
m
j
i N
i
N j
m
m
i N
j
j
i N
i
i
t
t
j i
G t
t
j i t
t
t
j i
−
=
−
−
−
=
=
⎧
≥ Ρ
⎪⎪
=
⎨
⎪
Ρ
−
< Ρ
⎪⎩
∑
∑
∑
Аналогично
для
произвольного
момента
времени
l
(
,
l
j
X t
l
= σ ≥
) получаем
( )
( )
1
1
1
1
,
( )
, ;
,
( )
, ,
m
j
l
i
l
i
m
j
l
i
l
i
l t
S t
j i
l
t
S t
j i
+
=
+
=
⎧
> ≥
Ρ
⎪⎪
σ =
⎨
⎪
<
Ρ
⎪⎩
∑
∑
и средняя доходность имеет вид
( )
( ) ( )
( )
( ) ( )
( )
1
1
1
1
1
1
1
1
, ,
( )
, ;
,
,
( )
, .
m
m
l
i
l
j
l
i
l
i
i
l
j
m
m
l
i
l
j
j
l
i
l
i
i
G t
j i
t
S t
j i
G t
S t
j i t
t
S t
j i
+
+
=
=
+
+
=
=
⎧
Ρ
≥
Ρ
⎪⎪
=
⎨
⎪
Ρ −
<
Ρ
⎪⎩
∑
∑
∑
∑
Рассмотрим некоторые примеры, иллюстрирующие описанные
выше правила оптимальной остановки для дискретных марковских
цепей.
1.
Последовательность независимых случайных величин, имею-
щих равномерное распределение на отрезке [1, m] (с точки зрения
рынка — полный хаос).
Матрица переходных вероятностей имеет вид
( , ) 1/ .
l
i j
m
Ρ =
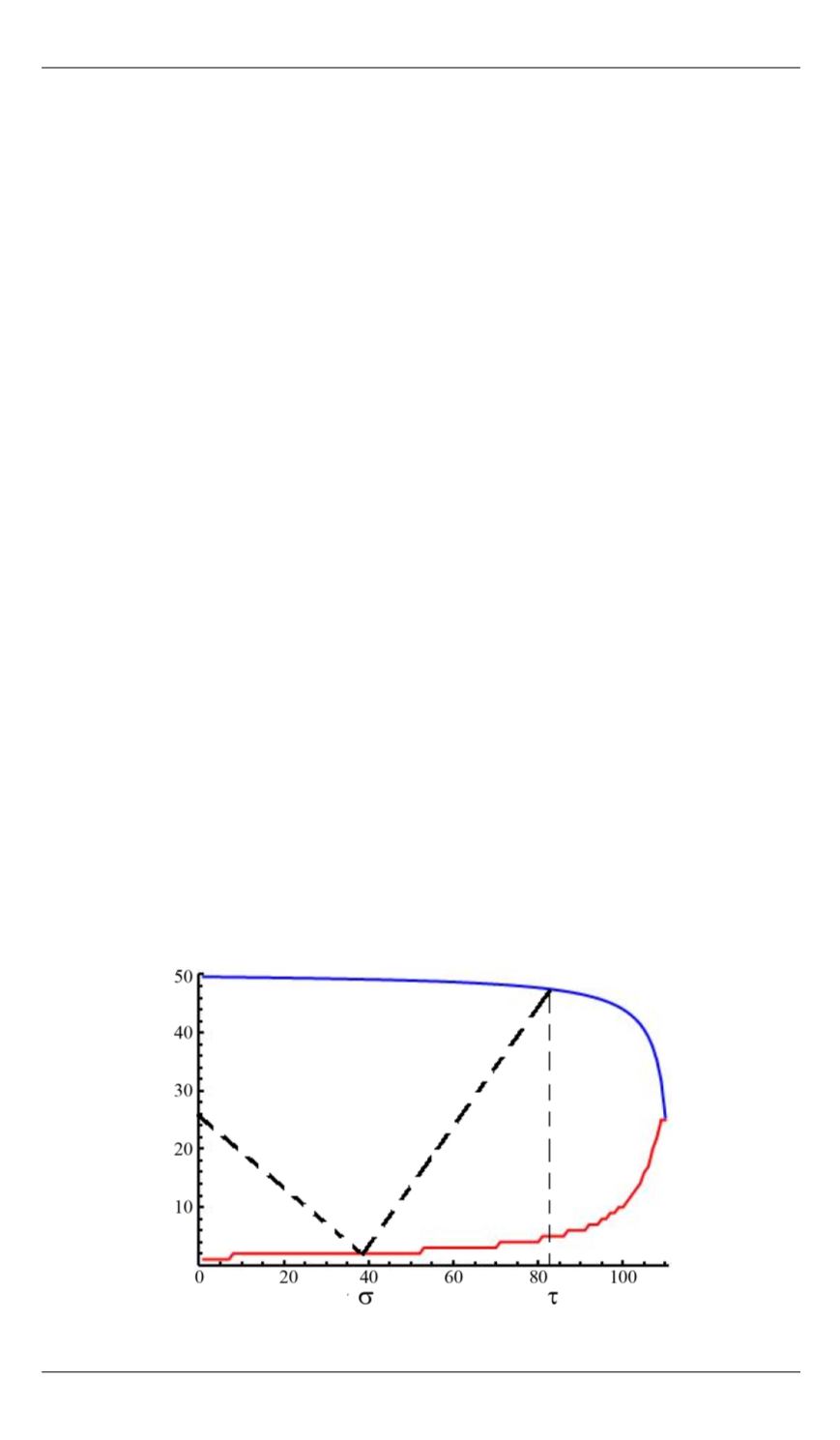
На рис. 1 представлены результаты расчетов для слу-
Рис. 1.
Оптимальные правила остановки для независимых случайных величин


