А.Ю. Карпачев
4
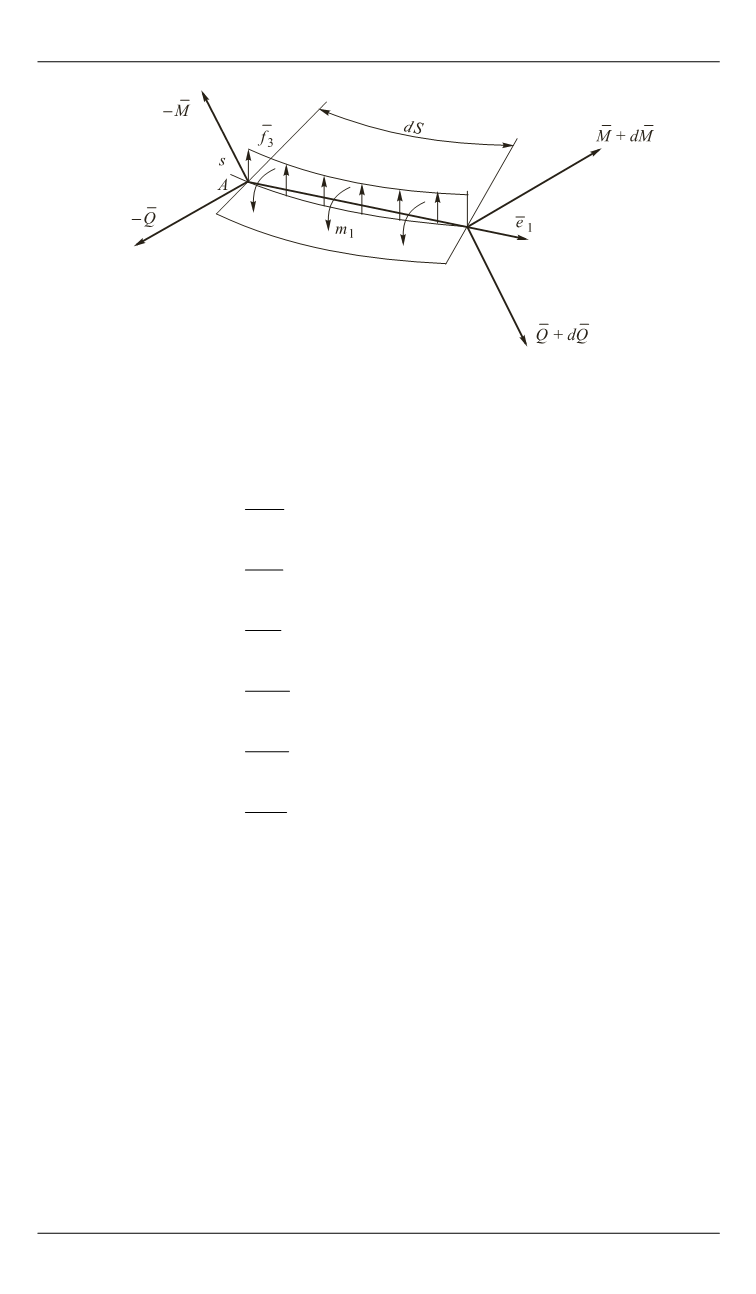
Рис. 2.
Расчетная схема системы сил, действующих на элемент стержня
Проецируя эти уравнения на оси, связанные с натуральным три-
эдром деформированного состояния стержня, получаем
2
1 1 3
3
1 2 2 1 3
1
2 3
2
2
1 1 3 3
3
1 2 2 1 2
1
2 3
2 1
δ
0,
δ δ
0,
δ
0,
δ
0,
δ
δ
0,
δ
0.
Q kQ Q
s
Q Q Q f
s
Q Q kQ
s
M kM M Q
s
M M M Q
s
M M kM m
s
∂
+ − =
∂
∂
+ − + =
∂
∂
+ − =
∂
∂
+ − − =
∂
∂
+ − + =
∂
∂
+ − + =
∂
(6)
Для дальнейших преобразований допустим, что результирующие
факторы, состоящие из факторов основного деформированного со-
стояния (индекс «o») от предварительного нагружения стержня, и
дополнительного (индекс «
∂
»), возникающие вследствие деформации
относительно первого состояния, имеют вид
o
,
i
i
i
Q Q Q
∂
= +
o
.
i
i
i
M M M
∂
= +
Факторы дополнительного состояния считаем малыми по сравнению
с соответствующими факторами основного состояния. Тогда, прини-
мая во внимание, что
o
o
o
3
2
1
0,
Q M M
= = =
систему (6) можно предста-
вить как


