А.Ю. Карпачев
2
дуги оси
(0
),
s L
≤ ≤
или в виде
( ),
i
i
x x s
=
1, 2.
i
=
Свяжем с осью
натуральный триэдр
0
,
i
e
где
0
1
e
— единичный вектор касательной к
оси стержня;
0
2
e
— единичный вектор главной нормали;
0
3
e
—
единичный вектор бинормали. Соприкасающуюся плоскость примем
совпадающей с плоскостью
1 2
x Оx
и соответственно с плоскостью
наибольшей жесткости поперечных сечений, имеющий две оси сим-
метрии. Вектор полной кривизны оси стержня в исходном состоянии
0
0
3
Ω ,
ke
=
где
k
— кривизна оси.
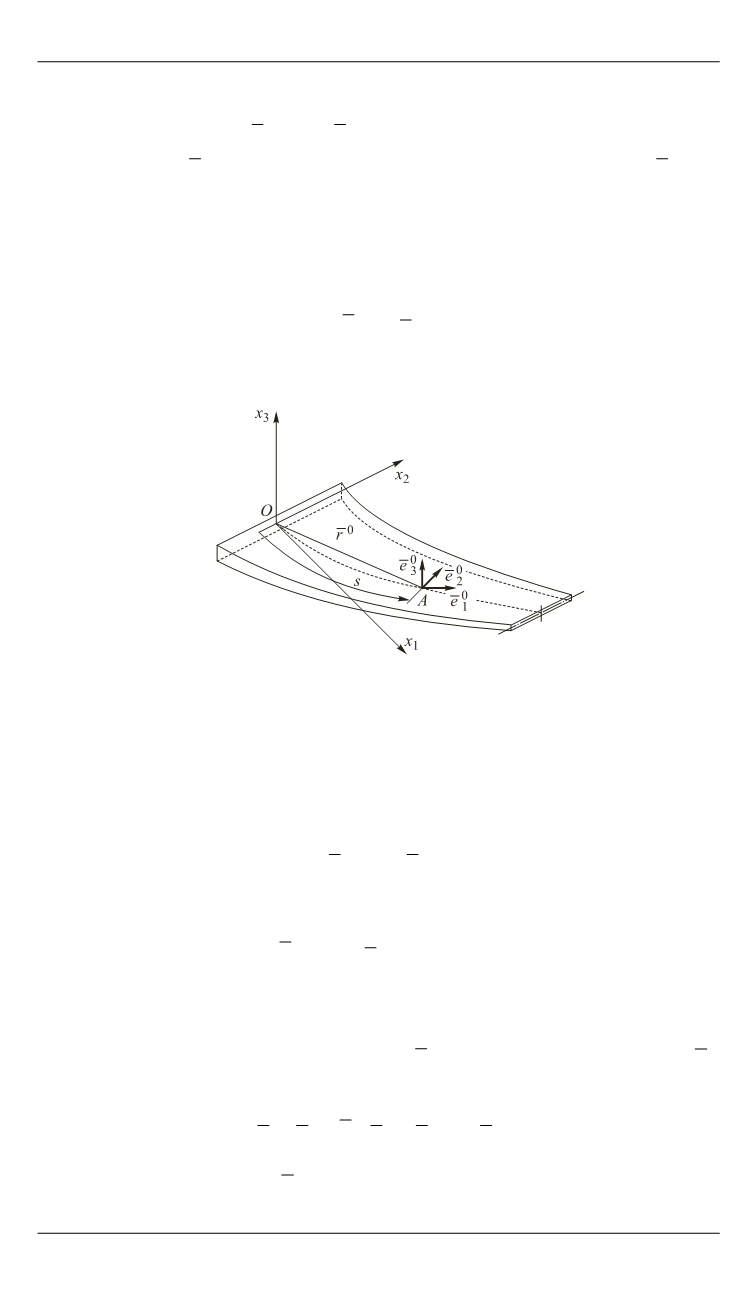
Рис. 1.
Расчетная схема стержня в виде полосы
Считаем, что отношение высоты наибольшего из сечений к длине
стержня намного меньше единицы. Для построения деформационных
соотношений воспользуемся гипотезой Бернулли. При этом за пере-
мещение точек оси стержня примем
0
3 3
( )
,
u s u e
=
а угол поворота сечения обозначим
0
( )
,
s
e
α α
ϑ = ϕ
1, 2,
α =
т. е. смещениями вдоль оси и главной нормали пренебрегаем, а также
не учитываем поворот сечений вокруг бинормали. Триэдр некоторого
сечения
A
займет новое положение
,
i
e
определяемое вектором
,
r
причем
0
0
0
0
1 1
1
1
2 3
.
e e
e e
e
= + ϑ× = −ϕ
(1)
Вместе с тем вектор
1
e
определяется соотношением


