Волны Фарадея в подвижном сосуде и их механический аналог
9
дов. Амплитуда тележки монотонно растет с уменьшением частоты
Ω
(рис. 5,
б
).
На рис. 5 также приведены результаты численного решения
уравнений движения (6) с использованием стандартной процедуры
NDSolve пакета Mathematica. В модели использовались эксперимен-
тальные характеристики маятника и тележки. В качестве коэффици-
ента трения качения взята величина
μ
= 0,02. Стационарные значения
амплитуд маятника и тележки (кривая
3
на рис. 5) получены только
для диапазона частот
Ω
= 9,125…11,80 с
–1
.
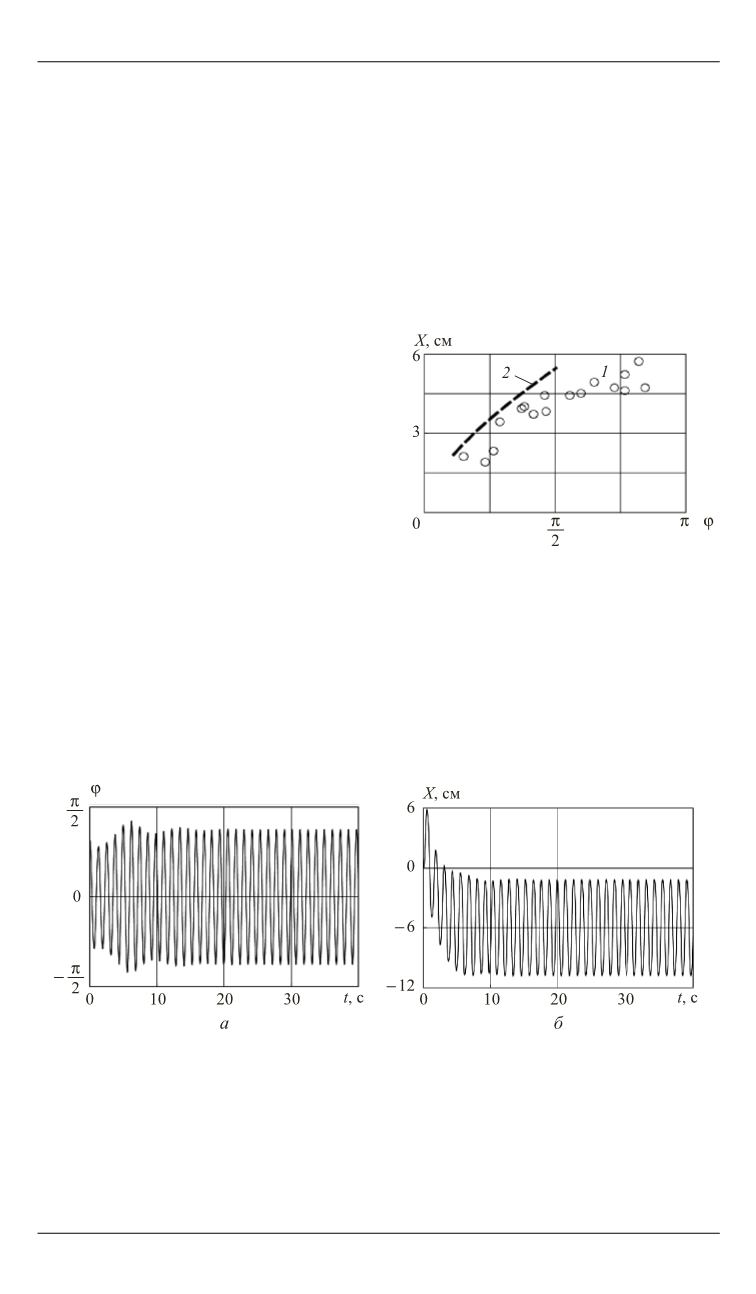
Рисунок 6 иллюстрирует взаи-
мосвязь колебаний маятника и те-
лежки. Ясно, что с увеличением
ϕ
амплитуда тележки также растет и
может достигать значительных ве-
личин порядка 6 см. Зависимость
2
,
полученная численным решением
системы (6), неплохо описывает
данные эксперимента при амплиту-
де маятника, не превышающей зна-
чение
/2.
π
Процесс установления стацио-
нарных колебаний при различных
значениях
Ω
показан на рис. 7. Переходный процесс характерен и
для маятника (
а
), и для тележки (
б
). Отмечается существенное сме-
щение положения, около которого происходят колебания тележки.
Эта особенность движения тележки наблюдалась и в эксперименте.
Рис. 7.
Схемы (
а
,
б
) процесса установления стационарных колебаний си-
стемы маятник — тележка по результатам численного решения первого и
второго уравнений (6) при
Ω
= 11,80; 10,50 с
–1
,
0
ϕ
= 0,88
0
(
x
= 0)
Заключение.
Экспериментально реализовано параметрическое
возбуждение гравитационных поверхностных волн в прямоугольном
сосуде при сохранении его горизонтальной степени свободы. Иссле-
Рис. 6.
Смещение тележки как
функция угла отклонения маятника:
эксперимент (
1
); численное реше-
ние уравнений (6) (
2
)


