В.А. Калиниченко, Аунг Наинг Со
8
Аналогичные результаты были получены при изменении экспе-
риментальных условий (для других значений
s
), что свидетельствует
о неплохом соответствии между моделью и экспериментом.
Теперь перейдем к параметрическому резонансу в механической
системе, состоящей из движущейся вдоль горизонтальной прямой
тележки массой
2
m
и подвешенного к ней маятника массой
1
m
(см.
рис. 1,
б
). Если ввести горизонтальную координату
x
тележки, дина-
мика плоского движения системы будет описываться уравнениями
2
1
2
1
1
2
2
1
1
1
(
) ( cos ) ( sin )
,
( cos )
(
cos ) sin
.
m m x m l
m l
F
m l
x m l
m l g s
t
b
′
+ +
ϕ ϕ =
ϕ ϕ −
ϕ + ϕ = − + Ω Ω ϕ − ϕ
(6)
Здесь
2
2
1
2
1
[(
)(
cos )
( sin
cos )]
F m m g s
t m l
′ = μ +
+ Ω Ω + ϕ ϕ + ϕ ϕ
— сила
трения качения между подшипниками тележки и горизонтальными
направляющими;
μ
— коэффициент трения качения.
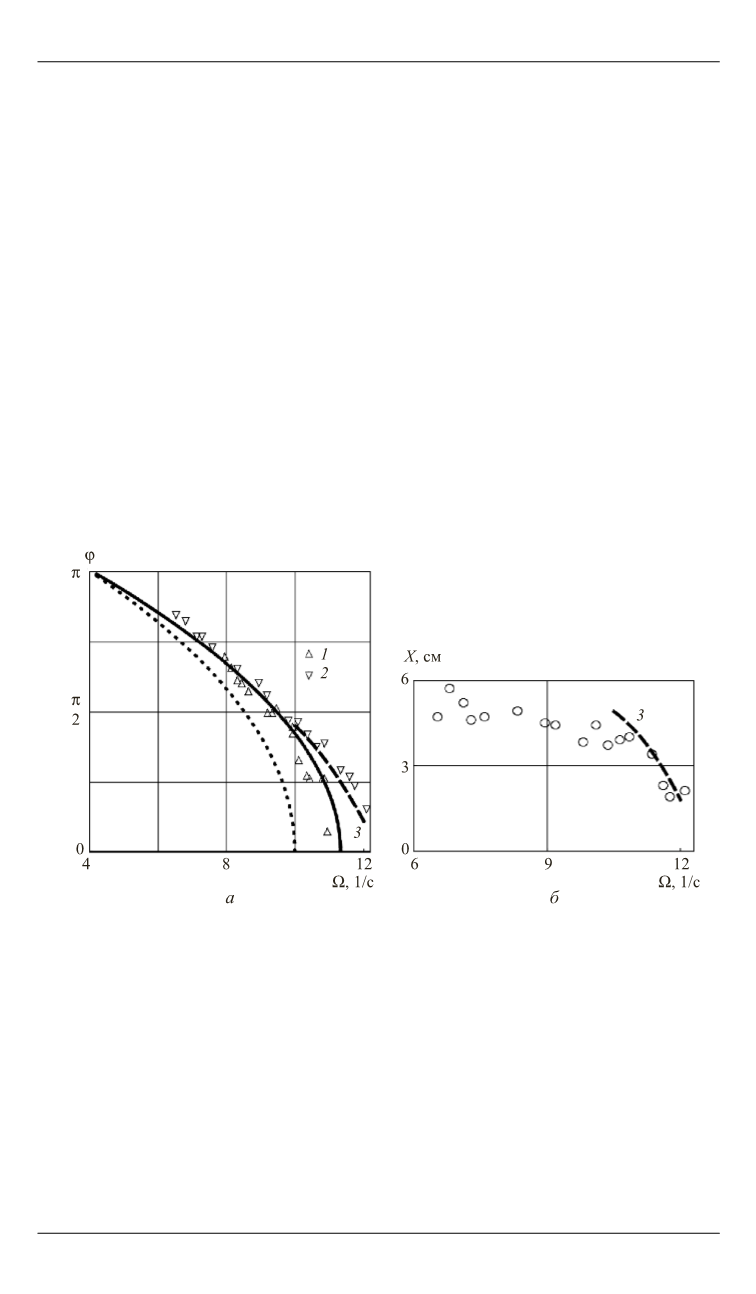
Амплитуды отклонения маятника и смещения тележки как функ-
ции частоты вертикальных колебаний приведены на рис. 5.
Рис. 5.
Отклонение маятника (
а
) и смещение тележки (
б
) в зависимости от
частоты вертикальных колебаний при
s
=
2,25 см: маятник
(
x
≡
0), теоре-
тическая модель (5) (
1
); маятник на тележке (
2
); численный расчет по
формуле (6) (
3
)
Анализ данных рис. 5,
а
показывает, что наличие тележки прак-
тически не влияет на колебания маятника. Отметим, что в случае ма-
ятника на тележке (
2
), согласно экспериментальным данным, проис-
ходит затягивание резонансной зависимости в область высоких ча-
стот
.
Ω
Кроме того, вблизи частоты срыва колебаний
Ω
= 6,51 с
–1
наблюдались перевороты маятника, повторяющиеся через 3–5 перио-


