Волны Фарадея в подвижном сосуде и их механический аналог
7
Отметим, что уравнение (1) для высоты
( )
H t
волны Фарадея и
уравнение (4), описывающее малые параметрические колебания ма-
ятника при
sin
ϕ
ϕ
, аналогичны. Данное обстоятельство использо-
валось в экспериментах [10] при изучении срыва параметрических
колебаний однородной и двухслойной жидкостей, обусловленного
разрушением волн Фарадея. В предложенной модели введен эквива-
лентный коэффициент затухания разрушающихся волн. Справедли-
вость принятого подхода продемонстрирована в экспериментах с од-
ной степенью свободы — с физическим маятником с вертикально ко-
леблющейся точкой подвеса.
Параметрическое возбуждение колебаний маятника происходит,
если расстройка
/ 2
Δ = ω− Ω
удовлетворяет условию
3
/ 8
s
g
Δ < Ω
.
Амплитуда
ϕ
m
стационарных колебаний маятника, согласно [15,
17], определяется уравнением
(
)
(
)
2
2
2
2
8(
2 ) 4
/
4 2 /
,
m
s g
b
±
− Ω − ω
ϕ =
± Ω −
ω
ω
(5)
где
ϕ
m
+
,
ϕ
m
–
отвечают устойчивой и неустойчивой ветвям резонанс-
ной зависимости соответственно.
На рис. 4 приведена резонансная
зависимость для маятника с коэффи-
циентом затухания
b
= 0,029 с
–1
при
s
= 1,05 см. После возбуждения ко-
лебаний на частоте
Ω
= 11,01 с
–1
их
амплитуда
ϕ
m
= 0,20 рад. При плав-
ном уменьшении частоты
Ω
ампли-
туда монотонно возрастала до мак-
симального значения:
m
ϕ
= 2,85 рад
при
Ω
= 5,04 с
–1
. Дальнейшее умень-
шение частоты
Ω
приводит
к срыву
колебаний при
Ω
= 4,97 с
–1
. Рассчи-
танные по формуле (5) ветви резо-
нансной зависимости пересеклись
при частоте срыва
Ω
= 4,91 с
–1
. Ес-
ли после срыва колебаний медленно
увеличивать частоту колебаний со-
суда, скачкообразное возбуждение
колебаний происходит при
Ω
=
= 10,25 с
–1
. Отметим, что представленная резонансная зависимость со-
ответствует случаю мягкой восстанавливающей силы.
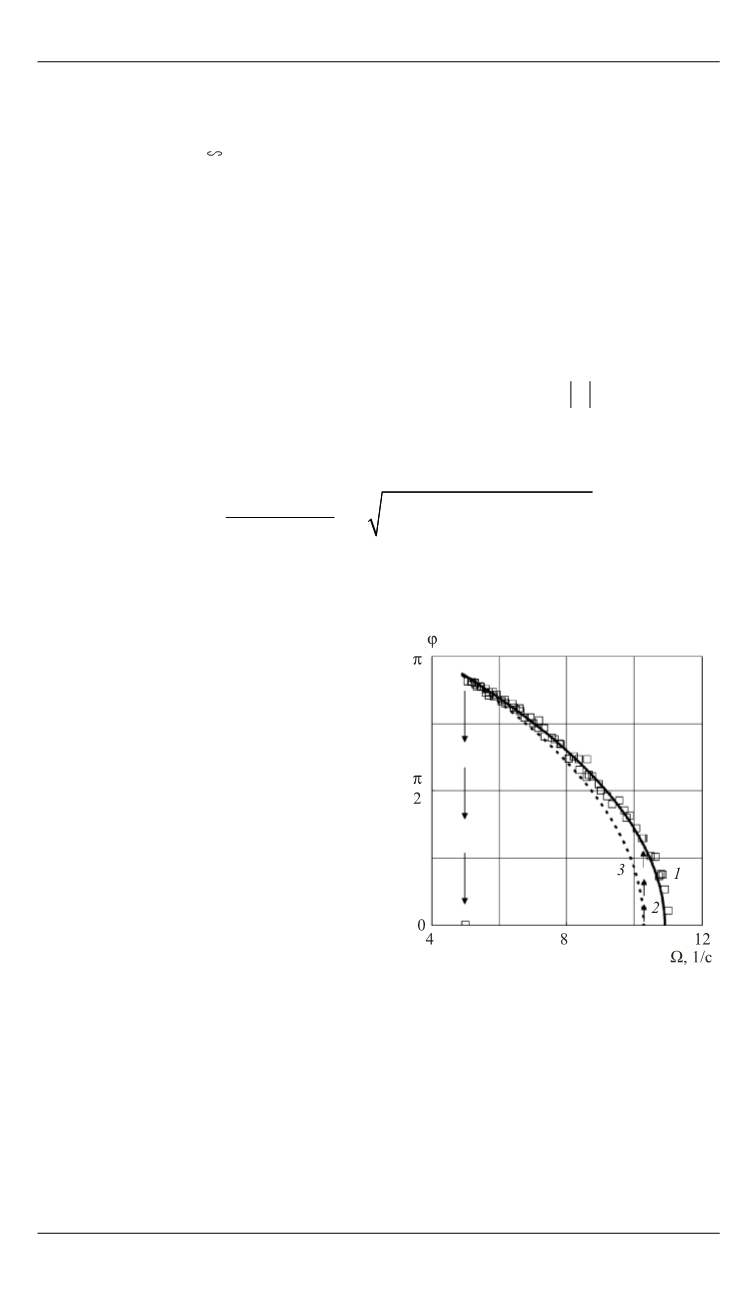
Рис. 4.
Резонансная зависимость
маятника (
s
=
1,05 см,
x
≡
0): экс-
перимент (
1
); устойчивая и не-
устойчивая ветви
( )
m
ϕ Ω
(
2
,
3
),
определяемые форм
у
лой (5)


