Н.Е. Зубов, Е.А. Микрин, В.Н. Рябченко
8
11
21
12
0 0 0 1 1
12
33
1
0 0 0 0
2 0
0 0
0 0 1
0 0
.
0
2 0 0
0 0 0 0 1
0 0 0 0
2
K h
h
K h
K h
D
K h h
K h
h
+
⎛
⎞
⎜
⎟
⎜
⎟
⎜
⎟
=
+ = ⎜
⎟
− ⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎝
⎠
B A B L B
Собственные значения матрицы
D
eig(
D
) в аналитическом виде
представляют собой очень громоздкие выражения для первых четы-
рех величин, которые обозначим
1 1
11 12 21 22 2
2
11 12 21 22
3 3
11 12 21 22
4
4
11 12 21 22
( ,
,
),
( ,
,
),
( ,
,
),
( ,
,
),
d f h K K K K d f h K K K K
d f h K K K K d f h K K K K
=
=
=
=
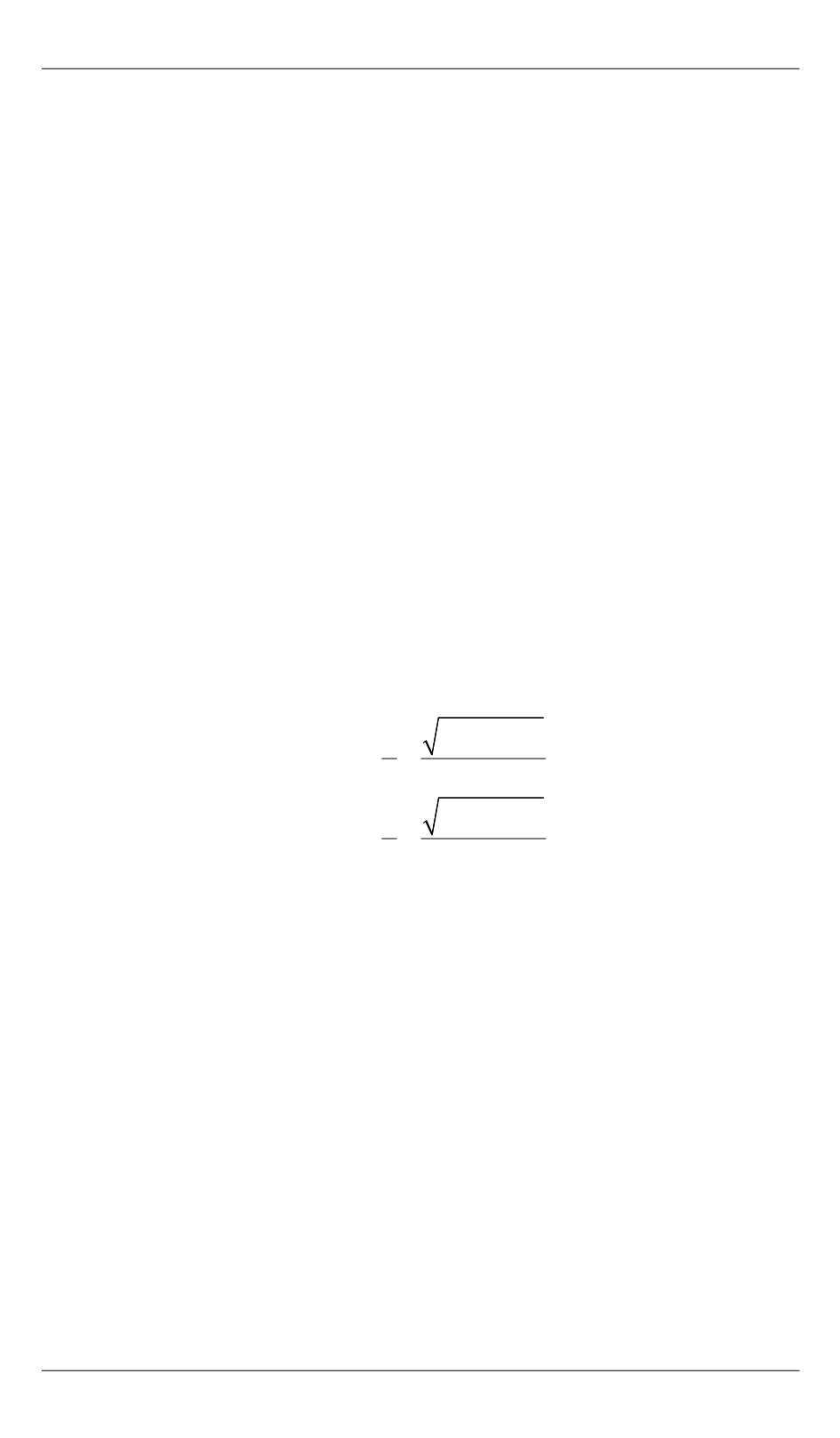
и в результате получим
1
2
3
4
2
33
2
33
eig( )
4
1
3
2
2
4
1
3
2
2
d
d
d
d
D
K h
K h
⎛
⎞
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
= ⎜
⎟
+
⎜
⎟
−
⎜
⎟
⎜
⎟
+
⎜
⎟
+ ⎜
⎟
⎝
⎠
.
В силу того, что собственные значения могут быть как положи-
тельными, так и отрицательными, то для обеспечения условия
нахождения внутри единичного круга
Φ
opt
—
D
поступим следующим
образом: назначим число
α
=
σ
и будем считать, что при этом обес-
печивается асимптотическая устойчивость матрицы
Φ
opt
и нахожде-
ние внутри единичного круга
Φ
opt
—
D
. Следовательно, значение
Φ
opt
—
D
определится выражением
11
21
22
opt
12
33
1
0 0 0 0
2
0
0 0
0
0 1
0 0
Ф
.
0
2
0 0
0
0
0 0 1
0
0
0 0
2
K h
h
K h
K h
K h h
K h
h
− σ ⎛
⎞
⎜
⎟
− σ
⎜
⎟
⎜
⎟
− σ
= ⎜
⎟
−
− σ
⎜
⎟
⎜
⎟
− σ
⎜
⎟
⎜
⎟ − σ
⎝
⎠
(19)


