Модель наблюдателя с использованием алгоритма оптимального размещения полюсов и ее применение в задачах управления космическим аппаратом - page 5

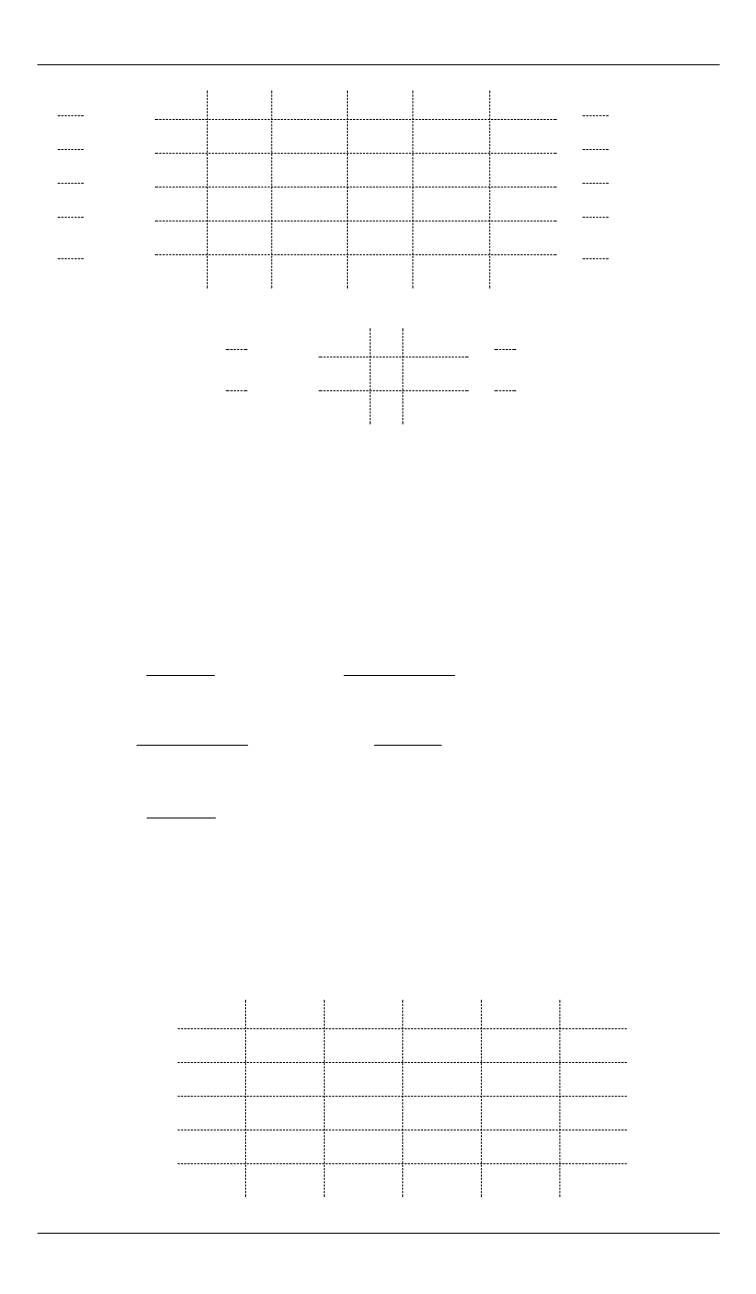
Модель наблюдателя с использованием алгоритма оптимального размещения полюсов…
5
11 11 12
0 0
21 22 22
0 0
1
1 0 0 0 0
1 0 0
0 0 1 0 0 0
0 0 0 1 0
0 0 1
0 0 0 0 0 1
n n
h
hK hK hK
h
hK hK hK
+
γ γ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
γ γ − −
⎜ ⎟ ⎜ ⎟
⎜ ⎟
⎜ ⎟ ⎜ ⎟ γ γ ⎜ ⎟
⎜ ⎟ ⎜ ⎟ = ⎜ ⎟
ψ ψ
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ − ψ ψ
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ψ ψ
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
, (11)
33 33
0 0
1
1 0
1
0 0 1
n n
K
h
h K h
+
θ θ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
θ = − θ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟ θ θ
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
, (12)
где γ, ψ, θ — углы отклонения связанного базиса КА относительно
орбитального в каналах крена, рыскания и тангажа; , , γ ψ θ — ско-
рости изменения указанных углов; γ0, ψ0, θ 0 — медленно меняющие-
ся углы в каналах крена, рыскания и тангажа, определяющие поло-
жение равновесия [5] относительно орбитального базиса; индекс n —
номер такта работы дискретной системы; h = 0,2 c — период кванто-
вания (длительность такта вычислений бортовой ЭВМ),
2
11 0 12 0
2
21 0 22 0
2
33 0
4 ; ;
; ;
3 ,
y z x y z
x x
x y z x z
y y
x y
z
J J J J J
K K
J J
J J J J J
K K
J J
J J
K
J
− + −
= ω = ω
+ − −
= ω = ω
−
= ω
где ω0 — орбитальная скорость КА на круговой орбите; Jx, J y, Jz —
моменты инерции КА относительно связанных осей.
Применим изложенный выше подход к решению задачи оценки
положения равновесной ориентации КА.
В соответствии с (2) и на основании (11), (12) имеем
11
21
11
T
22
12
22
1 0 0 0 0
1 0 0 0
0 1 0 0 0
,
0 0 0 1 0
0 0 1 0
0 0 0 0 1
hK
h hK
hK
hK
hK h
hK
γ−ψ
⎛ ⎞
⎜ ⎟
⎜ ⎟
⎜ ⎟ −
= ⎜ ⎟
⎜ ⎟
⎜ ⎟
−
⎜ ⎟
⎜ ⎟ −
⎝ ⎠
A (13)