Плотность одно- и двухчастичных состояний в кристаллах ниобата лития
9
0
0
1
1
1
1
1
1
( , )
( , ) (
,
),
a
a
k
d k d G k G k k
Π ω =
ω ω − ω−ω
∫ ∫
G
G
G
G G
(12)
и аналогично
33
( , )
k
Π ω
G
— свертка функций Грина разностных опти-
ческих фононов:
0
0
2
2
2
33
2
2
2
1
1
( , )
( ,
) (
,
) .
k
d k d G k
G k k
Π ω =
ω ω − ω − ω
∫ ∫
G
G
G
G G
(13)
Недиагональные компоненты поляризационного оператора соот-
ветствуют в данном случае резонансным трехфононным вершинам.
С учетом (2) константа связи
λ
3
формально имеет размерность квад-
рата частоты. Замкнутая система уравнений для четырех функций
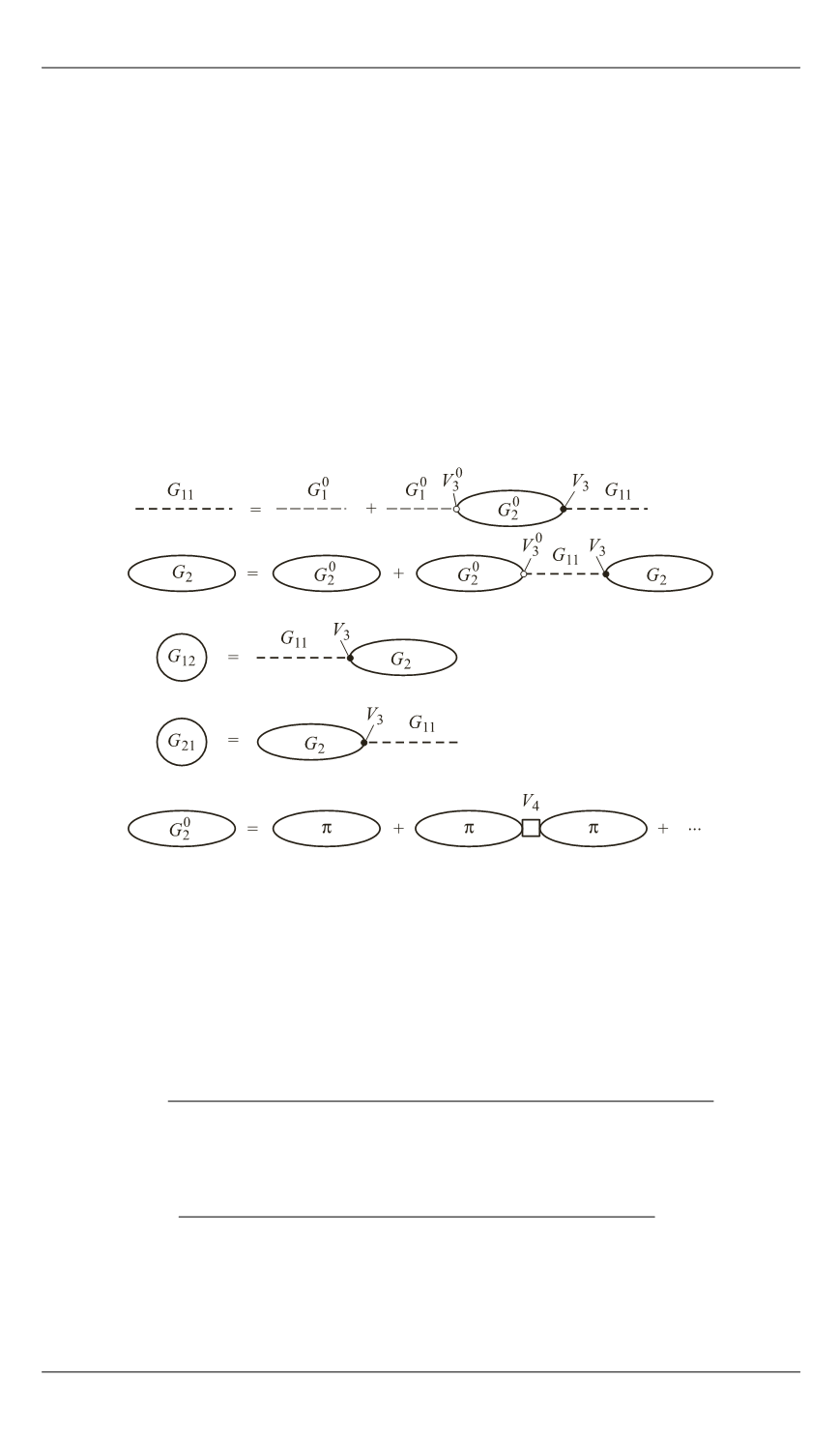
Грина представлена в виде диаграммы на рис. 2.
Рис. 2.
Представление уравнений для одно- и двухфононных функций Грина
Подставим найденные из уравнения (9) функции Грина в соот-
ношение (7). В результате получим
(ω)
(ω, ) 1
I
А n k
⎡
⎤
=
+ ×
⎣
⎦
G
( )
( ) ( )
( )
( )
( )
1 2
2 2
1 2
1
1
2
2
1 22
22
1 2
2 2
1
2
1
3
3
3
α
,ω 2α α
,ω ,ω α
,ω
Im
1
,ω ,ω
,ω ,
( )
( ) ( )
( )
( ) ( )
( ) ( ω)
G k
G k G k
G k
G k G k
G k G k
−
+
×
+
− λ
⎢
⎣
λ
⎡
−
⎢
G
G
G
G
G
G
G
G
( ) ( )
( )
( )
( )
1 2
2 2
1
3
3
1 34
34
1 2
2 2
1
2
1
3
3
3
2α α
,ω ,ω α
,ω
1
,ω ,
( ) ( )
( )
.
( ) ( )
( ) ( )
ω
,ω ,ω
G k G k
G k
G k G k
G k G k
⎤
−
+
+
⎥
⎥
− λ
− λ
⎦
G
G
G
G
G
G
G
(14)
Если предположить, что собственная интенсивность двухфонон-
ных переходов мала по сравнению с интенсивностью однофононных


